(本题满分14分)已知函数f(x)=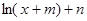
的图象在点(1，f(1))处的切线方程是
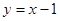，函数g(x)= 
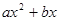(a、b∈R，a≠0)在x=2处取得极值-2．
(1)求函数f(x)、g(x)的解析式；
(2)若函数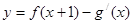
(其中
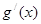是g(x)的导函数)在区间(
，
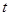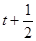)没有单调性，求实数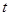的取值范围；
(3)设k∈Z，当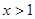
时，不等式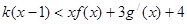
恒成立，求k的最大值．
已知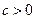
，设P：函数
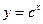在R上单调递减，Q：不等式
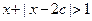的解集为R，如果P和Q有且仅有一个正确，求
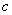的取值范围
求
的值
已知函数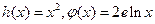
（其中e为自然对数）
（1）求F(x)=h(x)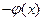
的极值。
（2）设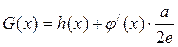
（常数a>0），当x>1时，求函数G(x)的单调区
间，并在极值存在处求极值。
设函数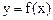
是定义在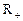
上的函数，并且满足下面三个条件：（1）对正数x、y都有
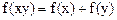；（2）当
时，
；（3）
。则
（Ⅰ）求
和
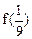的值；
（Ⅱ）如果不等式
成立，求x的取值范围．
（Ⅲ）如果存在正数k，使不等式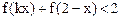
有解，求正数
的取值范围．
在如图所示的几何体中．EA⊥平面ABC，
DB⊥平面ABC，AC⊥BC，且AC＝BC＝BD＝2AE=2，M是AB的中点．
（Ⅰ）求证：CM⊥EM ；
（Ⅱ）求多面体ABCDE的体积
（Ⅲ）求直线DE与平面EMC所成角的正切值．