在等差数列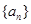 中,
中, ,且
,且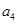 为
为 和
和 的等比中项,求数列
的等比中项,求数列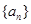 的首项、公差及前
的首项、公差及前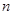 项和.
项和.
(本小题满分13分)已知数列 的首项
的首项 ,其前
,其前 和为
和为 ,且满足:
,且满足: (
( N*).
N*).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)对任意的 N*,
N*, ,求实数a的取值范围.
,求实数a的取值范围.
(本小题满分12分)如图,在长方体ABCD-A1B1C1D1中,AA1=AB=2AD=2,E为AB的中点,F为D1E上的一点,D1F=2FE.
(Ⅰ)证明:平面
 平面
平面 ;
;
(Ⅱ)求二面角 的平面角的余弦值.
的平面角的余弦值.
(本小题满分12分)某校举行中学生“珍爱地球·保护家园”的环保知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为 ,且相互间没有影响.
,且相互间没有影响.
(Ⅰ)求选手甲进入复赛的概率;
(Ⅱ)设选手甲在初赛中答题的个数为,试求的分布列和数学期望.
(本小题满分12分)在△ABC中,内角 ,
, ,
, 的对边长分别为a,b,c,且
的对边长分别为a,b,c,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若a=3, ,求△ABC的面积.
,求△ABC的面积.
(本小题满分14分)函数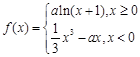 ,
,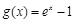 .
.
(Ⅰ)当a > 0时,求函数f (x)的极值;
(Ⅱ)当a在R上变化时,讨论函数f (x)与g (x)的图象公共点的个数;
(Ⅲ)求证: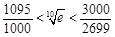 .(参考数据:
.(参考数据: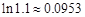 )
)