在△ABC中，角A，B，C所对的边分别是a，b，c．已知（b－2a）cosC＋c cosB＝0．
（1）求C；
（2）若c＝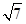
，b＝3a，求△ABC的面积．
计算由曲线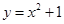
，直线x+y=3以及两坐标轴所围成的图形的面积S.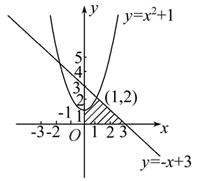
有5个男生和3个女生，从中选取5人担任5门不同学科的科代表，求分别符合下列条件的选法数：
(1)有女生但人数必须少于男生．
(2)某女生一定要担任语文科代表．
(3)某男生必须包括在内,但不担任数学科代表．
(4)某女生一定要担任语文科代表,某男生必须担任科代表,但不担任数学科代表．
已知复数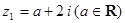
，
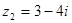，且
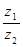为纯虚数，求复数
.
已知数列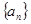
的前n项和为
，
＝1，且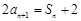
．
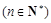（1）求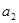
，
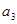的值，并求数列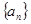的通项公式；
（2）解不等式
．
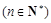已知圆C：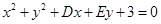
关于直线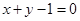
对称，圆心在第二象限，半径为
（1）求圆C的方程；
（2）是否存在斜率为2的直线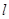
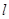，截圆C所得的弦为AB，且以AB为直径的圆过原点，若存在，则求出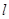的方程，若不存在，请说明理由.