本题共有2个小题，第1小题满分6分，第2小题满分8分
沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图，某沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8cm，细沙全部在上部时，其高度为圆锥高度的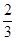
（细管长度忽略不计）．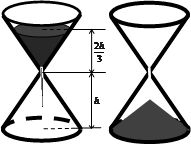
（1）如果该沙漏每秒钟漏下0.02cm3的沙，则该沙漏的一个沙时为多少秒（精确到1秒）？
（2）细沙全部漏入下部后，恰好堆成个一盖住沙漏底部的圆锥形沙堆，求此锥形沙堆的高度（精确到0.1cm）．
【改编】（本小题满分14分）已知数列
中，
，且点
（
）均在函数
的
图象上．
（1）求数列的通项公式；
（2）设
，求数列
的前
项和
．
（本小题满分14分）四棱锥
中，
底面
，
，
，
．
（1）求证：
平面
；
（2）若侧棱
上的点
满足
，求三棱锥
的体积．
【原创】（本小题满分12分）已知函数
（
）的最小正周期为
．
（1）求
的值；
（2）若
，
，求
的值．
【改编】（本小题满分14分）已知函数已知函数
（
，
）．
（1）当
时，求函数
在区间
上的最值；
（2）若
在区间
上单调递增，试求的取值范围．
（本小题满分14分）已知椭圆
的焦距为
，且过点
．
（1）求椭圆的方程；
（2）已知
，是否存在
使得点
关于
的对称点
（不同于点）在椭圆
上？若存在，求
出此时直线的方程；若不存在，说明理由．