(本小题满分13分)已知函数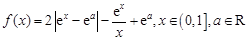
(1)当 时,求函数
时,求函数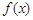 的单调区间;
的单调区间;
(2)当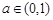 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式 .
.
(本小题满分12分)已知: 设
设 .
.
(1)求 的值;
的值;
(2)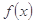 的展开式中的哪几项是有理项(回答项数即可);
的展开式中的哪几项是有理项(回答项数即可);
(3)求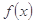 的展开式中系数最大的项和系数最小的项.
的展开式中系数最大的项和系数最小的项.
(本小题满分12分)已知 的顶点
的顶点 边上的中线
边上的中线 所在直线方程为
所在直线方程为 ,
, 边上的高
边上的高 所在直线方程为
所在直线方程为 .求
.求
(1)顶点 的坐标;
的坐标;
(2)直线 的方程.
的方程.
已知定义域为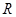 的函数
的函数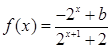 是奇函数。
是奇函数。
(1)求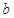 的值;
的值;
(2)判断函数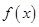 的单调性;
的单调性;
(3)若对任意的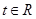 ,不等式
,不等式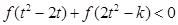 恒成立,求
恒成立,求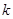 的取值范围.
的取值范围.
某种商品在最近40天内没见的销售价格 元与时间
元与时间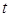 天的函数关系式是:
天的函数关系式是: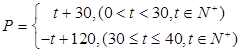 该商品的销售量
该商品的销售量 件与
件与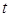 天的函数关系式是:
天的函数关系式是: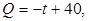

 ,求最近40天内这种商品的销售金额的最大值,并指出取得该最大值是第几天?
,求最近40天内这种商品的销售金额的最大值,并指出取得该最大值是第几天?
设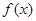 为二次函数,且
为二次函数,且 ,
,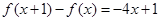 .
.
(1)求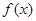 的解析式;
的解析式;
(2)设 ,若函数
,若函数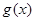 在实数
在实数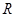 上没有零点,求
上没有零点,求 的取值范围.
的取值范围.