(本小题满分13分)等差数列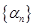 的前
的前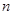 项和
项和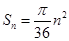 ,数列
,数列 满足
满足 .同学甲在研究性学习中发现以下六个等式均成立:
.同学甲在研究性学习中发现以下六个等式均成立:
①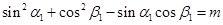 ;
;
② ;
;
③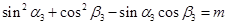 ;
;
④ ;
;
⑤ ;
;
⑥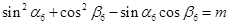 .
.
(1)求数列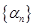 的通项公式,并从上述六个等式中选择一个,求实数
的通项公式,并从上述六个等式中选择一个,求实数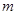 的值;
的值;
(2)根据(1)计算结果,将同学甲的发现推广为关于任意角 的三角恒等式,并证明你的结论.
的三角恒等式,并证明你的结论.
已知函数 .
.
⑴若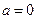 ,解方程
,解方程 ;
;
⑵若 ,求
,求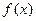 的单调区间;
的单调区间;
⑶若存在实数 ,使
,使 ,求实数
,求实数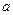 的取值范围 .
的取值范围 .
已知定义域为R的函数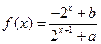 是奇函数。
是奇函数。
⑴求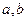 的值;并判定函数
的值;并判定函数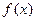 单调性(不必证明)。
单调性(不必证明)。
⑵若对于任意的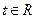 ,不等式
,不等式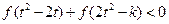 恒成立,求
恒成立,求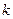 的取值范围。
的取值范围。
某租赁公司出租同一型号的设备40套,当每套月租金为270元时,恰好全部租出,在此基础上,每套月租金每增加10元,就少租出1套设备,而未租出的设备每月需支付各种费用每套20元,设每套设备实际月租金为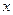
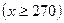 元,月收益为
元,月收益为 元(总收益=设备租金收入—未租出设备支出费用)。
元(总收益=设备租金收入—未租出设备支出费用)。
⑴求 与
与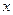 的函数关系式;
的函数关系式;
⑵当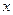 为何值时,月收益最大?最大月收益是多少?
为何值时,月收益最大?最大月收益是多少?
.已知函数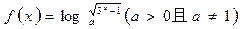
⑴求函数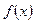 的定义域;
的定义域;
⑵求使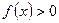 的
的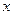 的取值范围。
的取值范围。
已知:全集 ,
,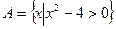 ,
,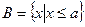 ;
;
⑴若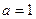 ,求
,求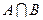 ,
,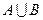 ;
;
⑵若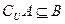 ,求:实数
,求:实数 的取值范围。
的取值范围。