(本小题满分12分)已知椭圆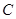 的中心在坐标原点,右焦点为
的中心在坐标原点,右焦点为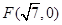 ,
,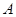 、
、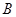 是椭圆
是椭圆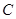 的左、右顶点,
的左、右顶点,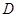 是椭圆
是椭圆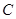 上异于
上异于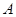 、
、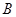 的动点,且
的动点,且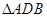 面积的最大值为12.
面积的最大值为12.
(1)求椭圆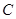 的方程;
的方程;
(2)求证:当点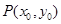 在椭圆
在椭圆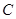 上运动时,直线
上运动时,直线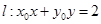 与圆
与圆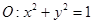 恒有两个交点,并求直线
恒有两个交点,并求直线 被圆
被圆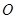 所截得的弦长
所截得的弦长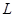 的取值范围.
的取值范围.
(本小题满分10分)△ABC中, 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且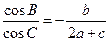 。
。
(1)求∠B的大小;
(2)若 =4,
=4, ,求
,求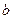 的值。
的值。
(本小题满分8分).已知△ABC中,A(2,4),B(-1,-2),C(4,3),BC边上的高为AD。
(1)求证: AB⊥AC;(2)求点D坐标。
(本小题满分8分)一货轮航行到M处,测得灯塔S在货轮的北偏东15°相距20里处,随后货轮按北偏西30°的方向航行,半小时后,又测得灯塔在货轮的北偏东45°,求货轮的速度。
(本小题满分8分)
已知两直线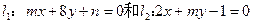 ,试确定
,试确定 的值,使得:
的值,使得:
(1)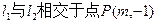 ;(2)
;(2)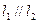
.已知函数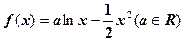 。(1)讨论函数
。(1)讨论函数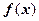 的单调性;(2)当
的单调性;(2)当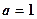 时,设
时,设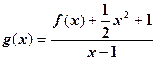 ,若
,若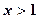 时,
时,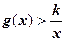 恒成立。求整数
恒成立。求整数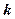 的最大值。
的最大值。