2a(3a﹣2b)
如图,两座建筑物 与 ,其地面距离 为 ,从 的顶点 测得 顶部 的仰角 ,测得其底部 的俯角 ,求建筑物 的高(结果保留根号)

2017年5月教育部统一组织了国家义务教育阶段质量监测考试.四川省部分小学四年级学生参加了科学测试,测试成绩评定为 、 、 、 四个等级,为了解此次科学测试成绩情况,相关部门从四川省农村、县镇、城市三类群体的学生中共抽取2000名学生的科学测试成绩进行分析,相关数据如表和图所示.
|
等级 人数 类别 |
|
|
|
|
|
农村 |
|
160 |
180 |
80 |
|
县镇 |
200 |
182 |
160 |
|
|
城市 |
240 |
|
122 |
48 |
(注:等级 , , , 分别代表优秀、良好、合格、不合格)
(1)请算出表中的 , , (直接填数据,不写解答过程);
(2)此次抽取的2000名学生的科学测试成绩为 等级的百分率是多少?
(3)若此次在四川省抽查的所有四年级学生中农村学生共有16000人,试估计抽查的农村学生科学测试成绩为 等级的大约有多少人?

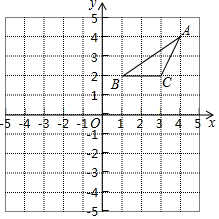
在边长为1个单位长度的正方形网格中建立如图的平面直角坐标系 , 的顶点都在格点上,请解答下列问题:
(1)将 向下平移5个单位长度,画出平移后的△ ;
(2)若点 是 内一点,其坐标为 ,点 在△ 内的对应点为 ,则点 的坐标为 ;
(3)画出 关于点 的中心对称图形△ .
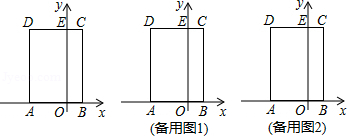
如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒1个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 的运动过程中,是否存在点 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.
为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买2个甲种文具、1个乙种文具共需花费35元;购买1个甲种文具、3个乙种文具共需花费30元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共120个,投入资金不少于955元又不多于1000元,设购买甲种文具 个,求有多少种购买方案?
(3)设学校投入资金 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?