2017年5月教育部统一组织了国家义务教育阶段质量监测考试.四川省部分小学四年级学生参加了科学测试,测试成绩评定为 、 、 、 四个等级,为了解此次科学测试成绩情况,相关部门从四川省农村、县镇、城市三类群体的学生中共抽取2000名学生的科学测试成绩进行分析,相关数据如表和图所示.
等级 人数 类别 |
|
|
|
|
农村 |
|
160 |
180 |
80 |
县镇 |
200 |
182 |
160 |
|
城市 |
240 |
|
122 |
48 |
(注:等级 , , , 分别代表优秀、良好、合格、不合格)
(1)请算出表中的 , , (直接填数据,不写解答过程);
(2)此次抽取的2000名学生的科学测试成绩为 等级的百分率是多少?
(3)若此次在四川省抽查的所有四年级学生中农村学生共有16000人,试估计抽查的农村学生科学测试成绩为 等级的大约有多少人?

某校为了了解九年级学生体育测试成绩情况,抽查了一部分学生的体育测试成绩,甲、乙、丙三位同学将抽查出的学生的测试成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下统计图,其中测试成绩在90~100分为A级,75~89分为B级, 60~74分为C级,60分以下为D级。甲同学计算出成绩为C的频率是0.2,乙同学计算出成绩为A、B、C的频率之和为0.96,丙同学计算出成绩为A的频数与成绩为B的频数之比
为7:12.结合统计图回答下列问题:这次抽查了多少人?
所抽查学生体育测试成绩的中位数在哪个等级内?
若该校九年级学生共有500人,请你估计这次体育测试成绩为A级和B级的学生共有多少人?

已知一次函数y=x+2与反比例函数 ,其中一次函数y=x+2的图象经过点P(k,5).
,其中一次函数y=x+2的图象经过点P(k,5).试确定反比例函数的表达式;
若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标.
如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.求证:△ABE≌△CAD;
求∠BFD的度数.

如图,在平面直角坐标系中,点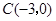 ,点
,点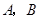 分别在
分别在 轴,
轴,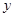 轴的正半轴上,且满足
轴的正半轴上,且满足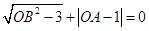 .
.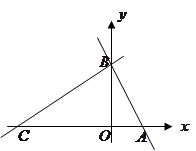
求点
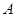 ,点
,点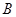 的坐标
的坐标若点
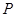 从
从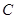 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段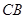 运动,连结
运动,连结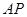 .设
.设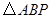 的面积为
的面积为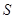 ,点
,点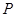 的运动时间为
的运动时间为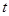 秒,求
秒,求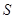 与
与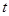 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.在(2)的条件下,是否存在点
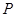 ,使以点
,使以点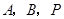 为顶点的三角形与
为顶点的三角形与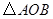 相似?若存在,请直接写出点
相似?若存在,请直接写出点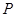 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图①,双曲线y=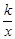 (k>0)与直线y=k'x交于A、B两点,点A在第一象限.
(k>0)与直线y=k'x交于A、B两点,点A在第一象限.若点A的坐标为(4,2),则点B的坐标为_______.若点A的横坐标为m,则点B的坐标可表示为_______.
如图②,过原点O作另一条直线l,交双曲线y=
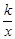 (k>0)于P、Q两点,点P在第一
(k>0)于P、Q两点,点P在第一
象限.①四边形APBQ的形状一定是
②设点A、P的横坐标分别为m、n,四边形APBQ可能是矩形吗?若可能,请直接写
出m、n应满足的条件;若不可能,请说明理由.