(本小题满分12分)某城市为准备参加“全国文明城市”的评选,举办了“文明社区”评选的活动,在第一轮暗访评分中,评委会对全市50个社区分别从“居民素质”和“社区服务”两项进行评分,每项评分均采用5分制,若设“社区服务”得分为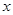 分,“居民素质”得分为
分,“居民素质”得分为 分,统计结果如下表:
分,统计结果如下表:
(1)若“居民素质”得分和“社区服务”得分均不低于3分(即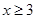 且
且 )的社区可以进入第二轮评比,现从50个社区中随机选取一个社区,求这个社区能进入第二轮评比的概率;
)的社区可以进入第二轮评比,现从50个社区中随机选取一个社区,求这个社区能进入第二轮评比的概率;
(2)若在50个社区中随机选取一个社区,这个社区的“居民素质”得1分的概率为 ,求
,求 、
、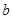 的值.
的值.
设 且
且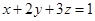
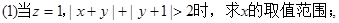
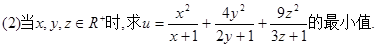
已知点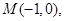 直线
直线 与曲线
与曲线
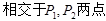 ,
,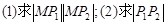
袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分 的分布列和数学期望.
的分布列和数学期望.
已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程 是否有实数解 .
是否有实数解 .
已知函数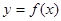 是定义域为
是定义域为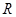 的奇函数,且当
的奇函数,且当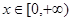 时,
时,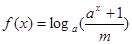 ,(
,( 。
。
(1)求实数 的值;并求函数
的值;并求函数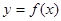 在定义域
在定义域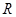 上的解析式;
上的解析式;
(2)求证:函数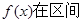
 上是增函数。
上是增函数。