(本小题满分14分)已知二次函数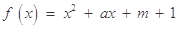 ,关于
,关于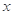 的不等式
的不等式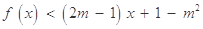 的解集为
的解集为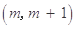 ,(
,(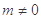 ),设
),设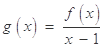 .
.
(1)求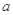 的值;
的值;
(2)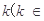 R
R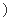 如何取值时,函数
如何取值时,函数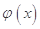
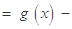
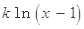 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且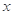
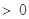 ,求证:
,求证: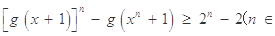 N
N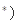 .
.
如图,四棱锥 的底面
的底面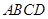 是正方形,
是正方形, 平面
平面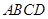 ,
, 为
为 上的点,且
上的点,且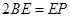 .
.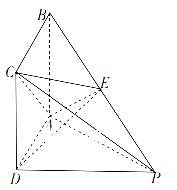
(1)证明: ;
;
(2)若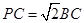 ,求二面角
,求二面角 的余弦值.
的余弦值.
为贯彻“激情工作,快乐生物”的理念,某单位在工作之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分,为了增加节目的趣味性,初赛采用选手选—题答—题的方式进行,每位选手最多有5次选答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题的正确率为 .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数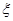 ,试写出
,试写出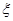 的分布列,并求
的分布列,并求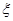 的数学期望。
的数学期望。
已知函数 ,
, .
.
(1)求 的值;
的值;
(2)设 、
、 ,
, ,
, ,求
,求 的值.
的值.
已知函数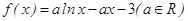 .
.
(I)若 ,求函数
,求函数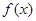 的单调区间;
的单调区间;
(Ⅱ)求证:
(Ⅲ)若函数 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为 ,对于任意的
,对于任意的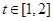 ,函数
,函数 是
是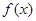 的导函数)在区间
的导函数)在区间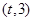 上总不是单调函数,求
上总不是单调函数,求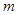 的取值范围。
的取值范围。
已知数列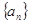 中,
中, 且点
且点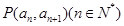 在直线
在直线 上。
上。
(1)求数列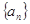 的通项公式;
的通项公式;
(2)若函数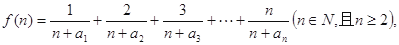 求函数
求函数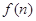 的最小值;
的最小值;
(3)设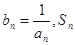 表示数列
表示数列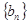 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式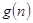 ,使得
,使得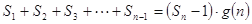 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立?若存在,写出
恒成立?若存在,写出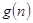 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。