(本小题满分10分)选修4-4:极坐标于参数方程
已知曲线 (
( 为参数),
为参数), (
( 为参数).
为参数).
(1)化 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若 上的点
上的点 对应的参数为
对应的参数为 ,
, 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
( 为参数)距离的最小值.
为参数)距离的最小值.
张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为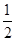 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
,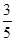 .
.
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数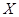 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你
帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.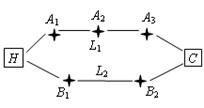
最近,某人准备将手中的10万块钱投资理财,现有二种方案:第一种方案:将10万块钱全部用来买股票,据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为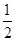 .第二种方案:将10万块钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可能损失10%,也可能不赔不赚,且三种情况发生的概率分别为
.第二种方案:将10万块钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可能损失10%,也可能不赔不赚,且三种情况发生的概率分别为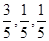 .针对以上两种投资方案,请你为选择一种合理的理财方法,并说明理由.
.针对以上两种投资方案,请你为选择一种合理的理财方法,并说明理由.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取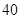 件产品作为样本称出它们的重量(单位:克),重量值落在
件产品作为样本称出它们的重量(单位:克),重量值落在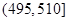 的产品为合格品,否则为不合格品.图
的产品为合格品,否则为不合格品.图 是甲流水线样本的频率分布直方图,表
是甲流水线样本的频率分布直方图,表 是乙流水线样本频数分布表.
是乙流水线样本频数分布表.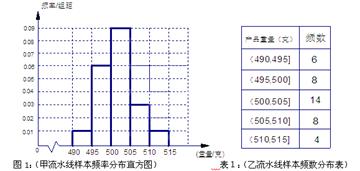
(Ⅰ) 若以频率作为概率,试估计从甲流水线上任取 件产品,求其中合格品的件数
件产品,求其中合格品的件数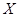 的数学期望;
的数学期望;
(Ⅱ)从乙流水线样本的不合格品中任意取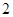 件,求其中超过合格品重量的件数
件,求其中超过合格品重量的件数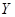 的分布列;
的分布列;
(Ⅲ)由以上统计数据完成下面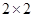 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关” .
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关” .
| 甲流水线 |
乙流水线 |
合计 |
|
| 合格品 |
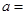 |
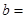 |
|
| 不合格品 |
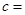 |
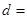 |
|
| 合 计 |
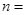 |
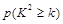 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
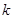 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
附:下面的临界值表供参考:
(参考公式: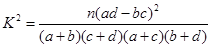 ,其中
,其中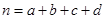 )
)
已知函数
(Ⅰ)若曲线 在点
在点 处的切线的倾斜角为
处的切线的倾斜角为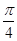 ,求实数
,求实数 的值;
的值;
(Ⅱ)若函数 在区间
在区间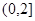 上单调递增,求实数实数
上单调递增,求实数实数 的范围.
的范围.
已知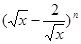 二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3.(I)求n的值;(II)求展开式中
二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3.(I)求n的值;(II)求展开式中 项的系数.
项的系数.