四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC 底面ABCD.已知
底面ABCD.已知 ABC=45o,AB=2,BC=2
ABC=45o,AB=2,BC=2 ,SA=SB=
,SA=SB= .
.
(1)证明:SA BC;
BC;
(2)求直线SD与平面SAB所成角的正弦值.
某选修课的考试按A级、B级依次进行,只有当A级成绩合格时,才可继续参加B级的考试.已知每级考试允许有一次补考机会,两个级别的成绩均合格方可获得该选修课的合格证书.现某人参加这个选修课的考试,他A级考试成绩合格的概率为 ,B级考试合格的概率为
,B级考试合格的概率为 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得该选修课的合格证书的概率;
(2)在这个考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,求
,求 的数学期望E
的数学期望E .
.
在 中,
中,
 .
.
(1)求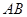 的值;
的值;
(2)求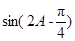 的值.
的值.
设函数 ,
, .
.
(1)解方程: ;
;
(2)令 ,求证:
,求证: ;
;
(3)若 是实数集
是实数集 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知数列 满足
满足 (
( 为常数,
为常数, )
)
(1)当 时,求
时,求 ;
;
(2)当 时,求
时,求 的值;
的值;
(3)问:使 恒成立的常数
恒成立的常数 是否存在?并证明你的结论.
是否存在?并证明你的结论.