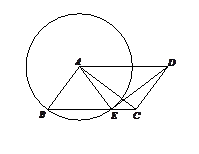“洛书”简介:
“洛书”是世界上最古老的一个三阶幻方,它有3行3列,三横行的三个数之和,三竖列的三个数之和,两对角线的三个数之和都等于15.其实幻方就是把一些有规律的数填在纵横格数都相等的正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等.
问题发现:
“洛书”中还有一些规律是可以总结的,如:
(1)在“洛书”中放在最中间的数5称为核心数,这个数的确定不是随便填上去的,是有一定方法可寻的,那么请你在图①中写出一条寻找核心数的方法.
(2)如果把图①中每一列三个数(从上到下)看做一个三位数,则这三个三位数之和等于它们的逆转数(从下到上)之和.
验证:每一列三个数(从上到下)组成的三位数之和即:438+951+276=1665,它们的逆转数(从下到上)三个三位数之和:834+159+672=1665.
依据上面的发现,你能提出什么样的问题?并验证你所提出的问题.
提出问题:
验证:
问题拓展:
怎样的九个数能构造成三阶幻方呢?
(1)将洛书中的九个数分别加上1可得:2,3,4,5,6,7,8,9,10.它们能否构造成一个三阶幻方?如果能,请在图②的格子中写出一种排列法.
(2)请你写一个能构成三阶幻方的九个数(区别于上述所举的数):
(3)请你总结一个一般性的结论:
如图, 中,
中, ,
,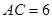 ,过点
,过点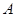 作
作 ∥
∥ ,点
,点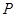 、
、 分别是射线
分别是射线 、线段
、线段 上的动点,且
上的动点,且 ,过点
,过点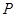 作
作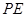 ∥
∥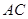 交线段
交线段 于点
于点 ,联接
,联接 ,设
,设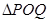 面积为
面积为 ,
,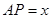 .
.
(1)用 的代数式表示
的代数式表示 ;
;
(2)求 与
与 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接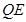 ,若
,若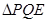 与
与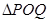 相似,求
相似,求 的长.
的长.
如图,在平面直角坐标系中,二次函数 的图像经过点
的图像经过点 ,
, ,
, ,顶点为
,顶点为 .
.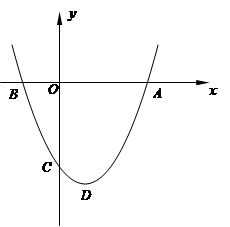
(1)求这个二次函数的解析式及顶点坐标;
(2)在 轴上找一点
轴上找一点 (点
(点 与点
与点 不重合),使得
不重合),使得 ,求点
,求点 坐标;
坐标;
(3)在(2)的条件下,将 沿直线
沿直线 翻折,得到
翻折,得到 ,求点
,求点 坐标.
坐标.
已知:如图,在 中,
中, ,
, 的平分线交
的平分线交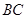 于
于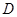 ,
,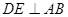 ,垂足为
,垂足为 ,连结
,连结 ,交
,交 于点
于点 .
.
(1)求证: ;
;
(2)如过点 作
作 ∥
∥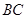 交
交 于点
于点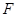 ,连结
,连结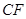 ,猜想四边形
,猜想四边形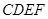 是什么图形?并证明你的猜想.
是什么图形?并证明你的猜想.
今年3月5日,光明中学组织全体学生参加了“走出校门,服务社会”的活动,活动分为打扫街道、去敬老院服务和到社区文艺演出三项。从九年级参加活动的同学中抽取了部分同学对打扫街道、去敬老院服务和到社区文艺演出的人数进行了统计,并做了如下直方图和扇形统计图。请根据两个图形,回答以下问题:
(1)抽取的部分同学的人数?
(2)补全直方图的空缺部分.
(3)若九年级有400名学生,估计该年级去敬老院的人数.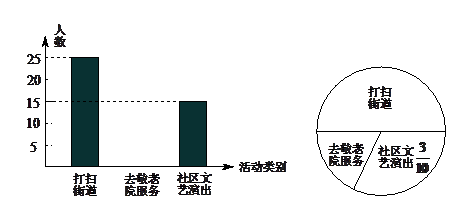
如图,在平行四边形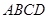 中,以点
中,以点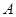 为圆心,
为圆心,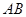 为半径的圆,交
为半径的圆,交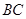 于点
于点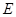 .
.
(1)求证: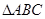 ≌
≌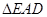 ;
;
(2)如果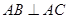 ,
,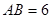 ,
,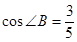 ,求
,求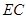 的长.
的长.