恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放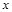 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为 元,试写出
元,试写出 与
与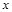 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
如图,已知反比例函数 的图象经过点 , 轴,且 的面积为2.
(1)求 和 的值;
(2)若点 也在反比例函数 的图象上,当 时,求函数值 的取值范围.

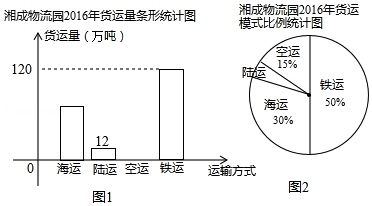
在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数.
甲、乙、丙三个同学站成一排进行毕业合影留念,请用列表法或树状图列出所有可能的情形,并求出甲、乙两人相邻的概率是多少?
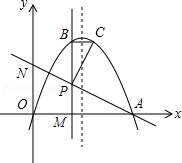
抛物线 与 轴相交于 、 两点(其中 为坐标原点),过点 作直线 轴于点 ,交抛物线于点 ,点 关于抛物线对称轴的对称点为 (其中 、 不重合),连接 交 轴于点 ,连接 和 .
(1) 时,求抛物线的解析式和 的长;
(2)如图 时,若 ,求 的值;
(3)是否存在实数 ,使 ?若存在,求出 的值,如不存在,请说明理由.
已知矩形 的一条边 ,将矩形 折叠,使得顶点 落在 边上的 点处
(Ⅰ)如图1,已知折痕与边 交于点 ,连接 、 、 .若 与 的面积比为 ,求边 的长.
(Ⅱ)如图2,在(Ⅰ)的条件下,擦去折痕 、线段 ,连接 .动点 在线段 上(点 与点 、 不重合),动点 在线段 的延长线上,且 ,连接 交 于点 ,作 于点 .试问当动点 、 在移动的过程中,线段 的长度是否发生变化?若变化,说明变化规律.若不变,求出线段 的长度.
