已知抛物线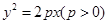 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4,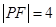 .
.
(1)求抛物线的方程;
(2)设点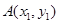 ,
, (
(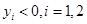 )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
已知数列 满足:
满足: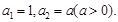 数列
数列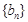 满足
满足 。
。
(1)若 是等差数列,且
是等差数列,且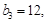 求
求 的值及
的值及 的通项公式;
的通项公式;
已知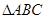 的周长为
的周长为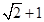 ,且
,且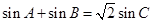
(1)求边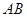 的长;
的长;
(2)若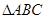 的面积为
的面积为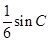 ,求角
,求角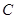 .
.
已知向量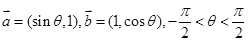 .
.
(1)若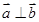 ,求
,求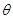 ;
;
(2)求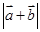 的最大值.
的最大值.
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) |
1 |
2 |
3 |
4 |
5 |
| 人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有 年多于10人的概率.
年多于10人的概率.
(2)根据这 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)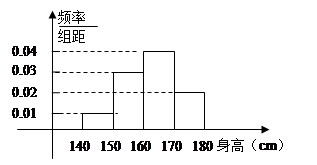
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
(2)在身高为140—160的学生中任选2个,求至少有一人的身高在150—160之间的概率.