已知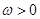 ,向量
,向量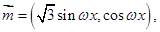 向量
向量 ,且
,且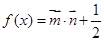 的最小正周期为
的最小正周期为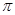 .
.
(1)求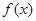 的解析式;
的解析式;
(2)已知 、
、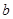 、
、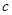 分别为
分别为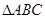 内角
内角 所对的边,且
所对的边,且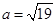 ,
,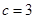 ,又
,又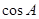 恰
恰
是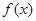 在
在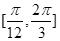 上的最小值,求
上的最小值,求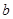 及
及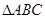 的面积.
的面积.
甲乙两班进行一门课程的考试,按照学生考试成绩的优秀和不优秀统计后得到如右的
列联表:
| 优秀 |
不优秀 |
总计 |
|
| 甲班 |
15 |
35 |
50 |
| 乙班 |
10 |
40 |
50 |
| 总计 |
25 |
75 |
100 |
(1)据此数据有多大的把握认为学生成绩优秀与班级有关?
(2)用分层抽样的方法在成绩优秀的学生中随机抽取5名学生,问甲、乙两班各应抽取多少人
(3)在(2)中抽取的5名学生中随机选取2名学生介绍学习经验, 求至少有一人来自乙班的概
率.(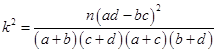 ,其中
,其中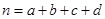 )
)
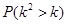 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
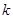 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知函数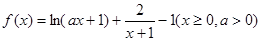 。
。
(1)若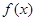 在
在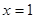 处取得极值,求
处取得极值,求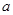 的值;
的值;
(2)求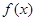 的单调区间;
的单调区间;
(3)若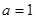 且
且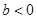 ,函数
,函数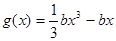 ,若对于
,若对于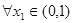 ,总存在
,总存在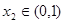 使得
使得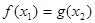 ,求实数
,求实数 的取值范围。
的取值范围。
两县城A和B相距20km,现计划在两县城外,以AB为直径的半圆弧AB上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与城B的影响度之和,记C点到城A的距离为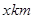 ,建在C处的垃圾处理厂对城A和城B的总影响度为
,建在C处的垃圾处理厂对城A和城B的总影响度为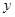 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。

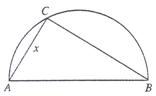
(1)将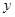 表示成
表示成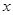 的函数;
的函数; (2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
已知函数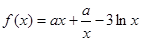 。
。
(1)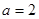 时,求
时,求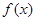 的最小值;
的最小值;
(2)若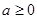 且
且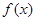 在
在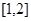 上是单调函数,求实数
上是单调函数,求实数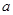 的取值范围。
的取值范围。