(本小题满分10分)选修4-1:几何证明选讲
如图,圆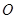 的直径
的直径 ,
,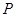 是
是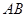 延长线上一点,
延长线上一点,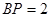 ,割线
,割线 交圆
交圆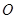 于点
于点 ,
,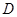 ,过点
,过点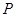 作
作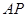 的垂线,交直线
的垂线,交直线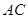 于点
于点 ,交直线
,交直线 于点
于点 .
.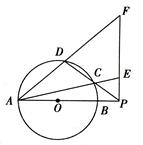
(1)求证: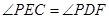 ;
;
(2)求 的值.
的值.
(本小题1 3分)
3分)
某公司要将一批不易存放的蔬菜从A地运到B 地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
| 运输工具 |
途中速度 (km/h) |
途中费用 (元/km) |
装卸时间 (h) |
装卸费用 (元) |
| 汽车 |
50 |
8 |
2 |
1000 |
| 火车 |
100 |
4 |
4 |
2000 |
若这批蔬菜在运输过程(含装卸时间)中损耗为300元/h,设A、B两地距离为 km
km
(I)设采用汽车与火 车运输的总费用分别为
车运输的总费用分别为 与
与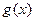 ,求
,求 与
与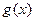 ;
;
(II)试根据A、B两地距离大小比较采用哪种运输工具比较好(即运输总费用最小).
(注:总费用=途中费用+装卸费用+损耗费用)
(本小题13分)
在正方体ABCD—A1B1C1D1中,M、N、G分别是A1A,D1C,AD的中点.
求证:(Ⅰ)MN//平面ABCD;(Ⅱ)MN⊥平面B1BG.
(本小题13分)
已知直线 过直线
过直线 和
和 的交点;
的交点;
(Ⅰ)若直线 与直线
与直线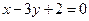 垂直,求直线
垂直,求直线 的方程.
的方程.
(Ⅱ)若原点 到直线
到直线 的距离为1.求直线
的距离为1.求直线 的方程.
的方程.
(本小题13分)
一个用鲜花做成的花柱,它的下面是一个直径为2m、高为4m的圆柱形物体,上面是一个直 径为2m的半球形体,如果每平方米大约需要鲜花200朵,那么装饰这个花柱大约需要多少朵鲜花(
径为2m的半球形体,如果每平方米大约需要鲜花200朵,那么装饰这个花柱大约需要多少朵鲜花(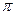 取3.1)?
取3.1)?
(本小题满分12分)
设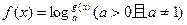
(1)若 在定义域D内是奇函数,求证:
在定义域D内是奇函数,求证: 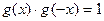 ;
;
(2)若
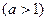 ,且在[1,3]上
,且在[1,3]上 的最大值是
的最大值是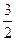 ,求实数
,求实数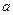 的值;
的值;
(3)在(2)的条件下,若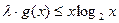 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.