用反证法证明“在同一平面内,若a⊥c,b⊥c,则a∥b”时,应假设( )
| A.a不垂直于c | B.a,b都不垂直于c | C.a⊥b | D.a与b相交 |
如图,点 分别是
分别是 各边的中点,下列说法中,错误的是()
各边的中点,下列说法中,错误的是()
A. 平分 平分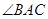 |
B.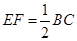 |
C. 与 与 互相平分 互相平分 |
D.△DEF是△ABC的位似图形 |
下列说法正确的是()
| A.分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,则△ADE是△ABC放大后的图形 |
| B.两位似图形的面积之比等于位似比 |
| C.位似多边形中对应对角线之比等于位似比 |
| D.位似图形的周长之比等于位似比的平方 |
下列说法不正确的是()
| A.位似图形一定是相似图形 |
| B.相似图形不一定是位似图形 |
| C.位似图形上任意一对对应点到位似中心的距离之比等于位似比 |
| D.位似图形中每组对应点所在的直线必相互平行 |
如图,小正方形的边长均为1,则右图中的三角形(阴影部分)与△ABC相似的是().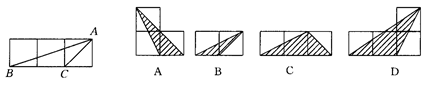
如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积()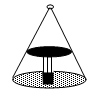
A.0.36 米2 米2 |
B.0.81 米2 米2 |
C.2 米2 米2 |
D.3.24 米2 米2 |