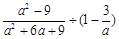如图,已知数轴上点A表示的数为8,B是数轴上的一点,AB=12,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ,经t秒后点P走过的路程为 (用含t的代数式表示);
(2)若在动点P运动的同时另一动点Q从点B也出发,并以每秒4个单位长度的速度沿数轴向左匀速运动,问经多长时间点P就能追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.
(本小题满分5分)某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题: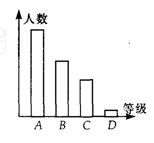
(1)共抽测了多少人?
(2)样本中B等级的频率是多少?
(3)如果要绘制扇形统计图,A等级在扇形统计图中所占的圆心角是多少度?
(4)该校九年级的毕业生共300人,假如“综合素质”等级为A或B的学生才能报考示范性高中,请你计算该校大约有多少名学生可以报考示范性高中?
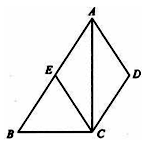
(本小题满分7分)如图,四边形 中,
中, ,
,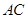 平分
平分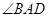 ,
,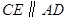 交
交 于
于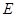 .
.
(1)求证:四边形
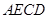 是菱形;
是菱形;(2)若点
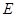 是
是 的中点,试判断
的中点,试判断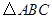 的形状,并说明理由.
的形状,并说明理由.
(本小题满分6分) 如图,平行四边形ABCD中,E、F是对角线BD上的点,且

求证: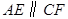
(本小题满分10分)解不等式组或方程(1)

(2)
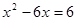
(本小题满分8分)计算或化简:(1)
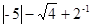 -
-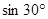 .
.(2)