(本小题满分12分)设椭圆 (a>b>0)的左右焦点分别为F1、F2,点D在椭圆上,DF1⊥F1F2,
(a>b>0)的左右焦点分别为F1、F2,点D在椭圆上,DF1⊥F1F2, ,△DF1F2的面积为
,△DF1F2的面积为 .
.
(1)求该椭圆的标准方程;
(2)若圆心在y轴上的圆与椭圆在x轴的上方有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点,求出这个圆的方程.
三棱柱 中,
中,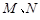 分别是
分别是 、
、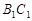 上的点,且
上的点,且 ,
, 。设
。设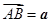 ,
, ,
, .
.
(Ⅰ)试用 表示向量
表示向量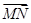 ;
;
(Ⅱ)若 ,
, ,
, ,求MN的长.。
,求MN的长.。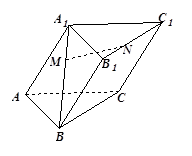
设命题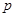 :方程
:方程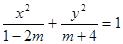 表示的图象是双曲线;命题
表示的图象是双曲线;命题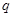 :
: ,
,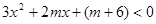 .求使“
.求使“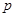 且
且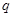 ”为真命题时,实数
”为真命题时,实数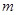 的取值范围.
的取值范围.
已知椭圆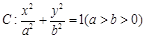 .
.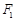 ,
,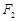 分别为椭圆
分别为椭圆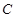 的左,右焦点,
的左,右焦点,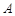
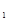 ,
,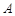
 分别为椭圆
分别为椭圆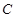 的左,右顶点.过右焦点
的左,右顶点.过右焦点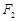 且垂直于
且垂直于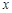 轴的直线与椭圆
轴的直线与椭圆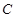 在第一象限的交点为
在第一象限的交点为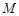
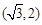 .
.
(1)求椭圆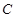 的标准方程;
的标准方程;
(2)直线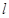
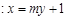 与椭圆
与椭圆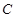 交于
交于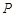 ,
,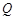 两点, 直线
两点, 直线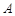
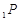 与
与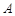
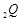 交于点
交于点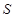 .当直线
.当直线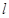 变化时, 点
变化时, 点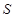 是否恒在一条定直线上?若是,求此定直线方程;若不是,请说明理由.
是否恒在一条定直线上?若是,求此定直线方程;若不是,请说明理由.
已知函数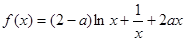 (a∈R).
(a∈R).
(1)当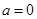 时,求
时,求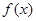 的极值;
的极值;
(2)当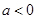 时,求
时,求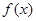 单调区间;
单调区间;
(3)若对任意 及
及 ,恒有
,恒有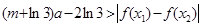
成立,求实数m的取值范围.
设数列 满足条件:
满足条件: ,
,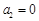 ,
,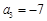 ,且数列
,且数列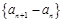
 是等差数列.
是等差数列.
(1)设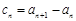 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若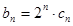 , 求
, 求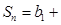
 ;
;
(3)数列 的最小项是第几项?并求出该项的值.
的最小项是第几项?并求出该项的值.