(本小题满分14分)已知圆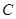 :
: 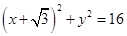 及点
及点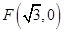 ,
,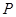 为圆
为圆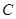 上一动点,在同一坐标平面内的动点M满足:
上一动点,在同一坐标平面内的动点M满足: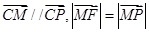 .
.
(Ⅰ)求动点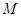 的轨迹
的轨迹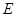 的方程;
的方程;
(Ⅱ)设过定点 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,且
,且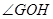 为锐角(其中
为锐角(其中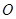 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率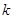 的取值范围.
的取值范围.
(Ⅲ)设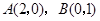 是它的两个顶点,直线
是它的两个顶点,直线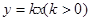 与
与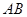 相交于点
相交于点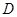 ,与椭圆相交于
,与椭圆相交于 两点.求四边形
两点.求四边形 面积的最大值
面积的最大值
已知函数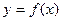 的定义域为R,对任意
的定义域为R,对任意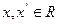 ,均有
,均有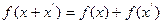 ,且对任意
,且对任意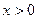 都有
都有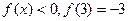 。
。
(1)试证明:函数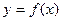 在R上是单调函数;
在R上是单调函数;
(2)判断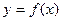 的奇偶性,并证明。
的奇偶性,并证明。
(3)解不等式 。
。
(4)试求函数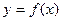 在
在 上的值域;
上的值域;
一片森林原来面积为 ,计划每年砍伐一些树,且每年砍伐面积的百分比
,计划每年砍伐一些树,且每年砍伐面积的百分比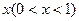 相等,当砍伐到面积的一半时,所用时间是10年。为保护生态环境,森林面
相等,当砍伐到面积的一半时,所用时间是10年。为保护生态环境,森林面
积至少要保留原来面积的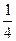 。已知到今年为止,森林剩余面积为原来的
。已知到今年为止,森林剩余面积为原来的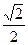 。
。
(1)求每年砍伐面积的百分比(用式子表示);
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
已知函数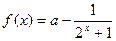 。
。
(1)求证:不论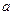 为何实数,
为何实数,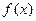 在R上总为增函数;
在R上总为增函数;
(2)确定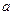 的值,使
的值,使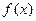 为奇函数;
为奇函数;
设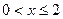 ,求函数
,求函数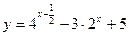 的值域。
的值域。
(1)画出函数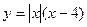 的图象;
的图象;
(2)利用图象回答: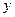 取何值时①只有唯一的
取何值时①只有唯一的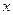 值与之对应?②有两个
值与之对应?②有两个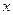 值与之对应?
值与之对应?
③有三个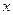 值与之对应?
值与之对应?