(本小题满分12分)2015国际滑联世界花样滑冰锦标赛于3月23日至29日在上海举行,为调查市民喜欢这项赛事是否与年龄有关,随机抽取了55名市民,得到如下数据表:
| 喜 欢 |
不 喜 欢 |
合 计 |
|
| 大于40岁 |
20 |
5 |
25 |
| 20岁至40岁 |
10 |
20 |
30 |
| 合 计 |
30 |
25 |
55 |
(Ⅰ)判断是否有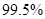 的把握认为喜欢这项赛事与年龄有关?
的把握认为喜欢这项赛事与年龄有关?
(Ⅱ)用分层抽样的方法从喜欢这项赛事的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
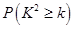 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
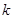 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: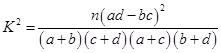 ,其中
,其中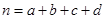 )
)
已知二次函数 .
.
(1)若 ,试判断函数
,试判断函数 零点个数
零点个数
(2)若对 且
且 ,
, ,证明方程
,证明方程 必有一个实数根属于
必有一个实数根属于 。
。
(3)是否存在 ,使
,使 同时满足以下条件①当
同时满足以下条件①当 时, 函数
时, 函数 有最小值0;;②对任意实数x,都有
有最小值0;;②对任意实数x,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
已知函数 , 其中
, 其中 为常数,且函数
为常数,且函数 图像过原点.
图像过原点.
求 的值;
的值;
(1)证明:函数 在[0,2]上是单调递增函数;
在[0,2]上是单调递增函数;
(2)已知函数 , 求g(x)≥0时x的取值范围。.
, 求g(x)≥0时x的取值范围。.
如图,正方形 的边长为1,正方形
的边长为1,正方形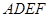 所在平面与平面
所在平面与平面 互相垂直,
互相垂直,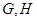 是
是 的中点.
的中点.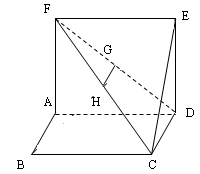
(1)求证: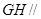 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
求经过直线 与直线
与直线 的交点M,且分别满足下列条件的直线方程:
的交点M,且分别满足下列条件的直线方程:
(1)与直线 平行;
平行;
(2)与直线 垂直.
垂直.
如图所示,一个空间几何体的正视图,侧视图,俯视图为全等的等腰直角三角形,,如果直角三角形的直角边边长都为1.
(1)画出几何体的直观图(不要求写出做图过程);
(2)求几何体的表面积和体积