(本小题满分12分)已知广东省某校高三(1)班有 名学生,从中按照系统抽样的方法抽取
名学生,从中按照系统抽样的方法抽取 名学生.
名学生.
(1)若第 组抽出的号码为
组抽出的号码为 ,写出所有被抽出学生的号码;
,写出所有被抽出学生的号码;
(2)分别统计这 名学生某高校自主招生考试成绩(满分:
名学生某高校自主招生考试成绩(满分: 分),获得成绩数据的茎叶图如图所示,现从这
分),获得成绩数据的茎叶图如图所示,现从这 名学生中随机抽取
名学生中随机抽取 名学生成绩,其中有
名学生成绩,其中有 名学生的成绩是超过
名学生的成绩是超过 的,求
的,求 的分布列与期望.
的分布列与期望.
已知函数f(x)=cos(-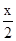 )+cos(
)+cos( ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的减区间;
(3)若f(α)= ,α∈(0,
,α∈(0,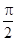 ),求tan(2α+
),求tan(2α+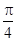 )的值.
)的值.
在△ABC中,角A、B、C所对的边分别为a、b、c,向量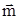 =
=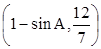 ,
, =(cos2A,2sinA),且
=(cos2A,2sinA),且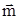 ∥
∥ .
.
(1)求sinA的值;
(2)若b=2,△ABC的面积为3,求a.
等比数列 中,
中,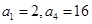 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若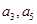 分别为等差数列
分别为等差数列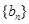 的第4项和第16项,求数列
的第4项和第16项,求数列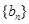 的前
的前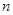 项和
项和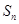 .
.
某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2 000平方米的楼房,经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
设函数f(x)=x3-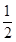 ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是单调函数,求a的取值范围;
(2)若a=2,且当x∈[1,2]时,f(x)≤m恒成立,求实数m的取值范围.