（本小题满分12分）如图，矩形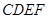
所在平面与直角梯形
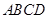所在平面垂直，其中
，
，
，
，
．
、
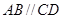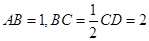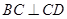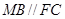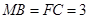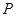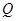分别为
、
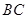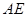的中点．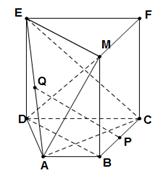
（1）求证：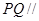
平面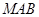
；
（2）求二面角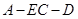
的余弦值．
已知函数
．
（Ⅰ）当
时，求函数
的极值；
（Ⅱ）若函数在定义域上没有零点，求实数
的取值范围.
投资商到一开发区投资72万元建起一座蔬菜加工厂，经营中，第一年支出12万元，以后每年支出增加4万元，从第一年起每年蔬菜销售收入50万元，设
表示前n年的纯利润总和（
前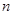
年总收入 前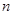年的总支出 投资额72万元）
（Ⅰ）该厂从第几年开始盈利？
（Ⅱ）该厂第几年平均纯利润达到最大？并求出年平均纯利润的最大值.
“坐标法”是以坐标系为桥梁，把几何问题转化成代数问题，通过代数运算研究图形的几何性质的方法，它是解析几何中是基本的研究方法. 请用坐标法证明下面问题：
已知圆O的方程是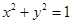
，点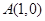
，P、Q是圆O上异于A的两点.证明：弦PQ是圆O直径的充分必要条件是
.
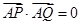已知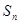
是等比数列{
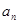}的前
项和，
、
、
成等差数列.
(Ⅰ)求数列{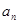}的公比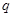
；
(Ⅱ)求证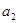
、
、
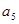成等差数列.
已知椭圆C的两焦点分别为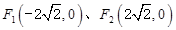
，长轴长为6.
（Ⅰ）求椭圆C的标准方程;
（Ⅱ）已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.