(本小题满分10分)选修4—5:不等式选讲
(Ⅰ)若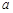 ,
,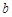 ,均为正数,且
,均为正数,且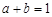 .证明:
.证明: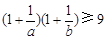 ;
;
(Ⅱ)设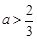 ,且
,且 时,
时,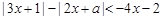 ,求实数
,求实数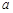 的取值范围.
的取值范围.
(满分10分)从社会效益和经济效益出发,某市决定投入资金进行生态环境建设,并以此发展旅游产业,打算本年度投入800万元,以后每年投入将比上年平均减少 ,本年度旅游收入为400万元,由于该项建设对旅游的促进作用,预计今后的旅游业收入每年会比上年平均增加
,本年度旅游收入为400万元,由于该项建设对旅游的促进作用,预计今后的旅游业收入每年会比上年平均增加 .
.
(Ⅰ)设第 年(本年度为第一年)的投入为
年(本年度为第一年)的投入为 万元,旅游业收入为
万元,旅游业收入为 万元,写出
万元,写出 和
和 的表达式;
的表达式;
(Ⅱ)至少经过几年旅游业的总收入超过总投入?
(满分10分)在△ 中,
中, 分别为内角A,B,C所对的边长,
分别为内角A,B,C所对的边长,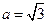 ,
, ,
,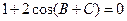 ,求边BC上的高.
,求边BC上的高.
(满分10分) 设 ,式中
,式中 满足条件
满足条件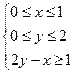 ,求
,求 的最大值和最小值。
的最大值和最小值。
(满分10分)记关于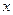 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式 的解集为
的解集为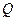 .
.
(I)若 ,求
,求 ;
;
(II)若 ,求正数
,求正数 的取值范围.
的取值范围.
已知
 ,向量
,向量 ,
,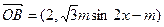 ,
, , 其中
, 其中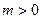 。
。
(1)求 的单调增区间;
的单调增区间;
(2)当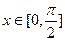 时,
时, 的最大值为5,求
的最大值为5,求 的值。
的值。