(本小题满分15分)如图,四棱锥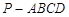 的底面
的底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
,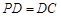 ,
,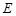 是
是 的中点.
的中点.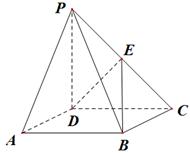
(Ⅰ)证明: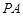 //平面
//平面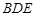 ;
;
(Ⅱ)求二面角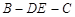 的平面角的余弦值;
的平面角的余弦值;
(Ⅲ)在棱 上是否存在点
上是否存在点 ,使
,使 ⊥平面
⊥平面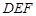 ?证明你的结论.
?证明你的结论.
设函数f (x)=2cosx (cosx+ sinx)-1, x∈R.
sinx)-1, x∈R.
(1)求f (x)的最小正周期T及单调递增区间;
(2)在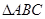 中,
中,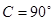 ,求f (A)的取值范围.
,求f (A)的取值范围.
已知函数 ,
,
(1)求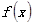 的单调区间和极值。 (2)求
的单调区间和极值。 (2)求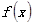 在
在 上的最大值和最小值。
上的最大值和最小值。
已知函数f(x)=alnx-x2+1.
(1)若曲线y=f(x)在x=1处的切线方程为4x-y+b=0,求实数a和b的值;
(2)若a<0,且对任意x1、x2∈(0,+∞),都|f(x1)-f(x2)|≥|x1-x2|,求a的取值范围.
三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两个岗位没有被选的概率;
(2)设选择A岗位的人数为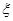 ,求
,求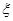 的分布列及数学期望。
的分布列及数学期望。
数列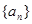 ,满足
,满足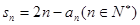
(1)求 ,并猜想通项公式
,并猜想通项公式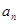 。
。
(2)用数学归纳法证明(1)中的猜想。