如图，将边长为4的等边三角形AOB放置于平面直角坐标系xOy中，F是AB边上的动点（不与点A，B重合），过点F的反比例函数
（
，
）与OA边交于点E，过点F作FC⊥x轴于点C，连接EF，OF．
（1）若
，求反比例函数的解析式．
（2）在（1）的条件下，试判断以点E为圆心，EA长为半径的圆与
轴的位置关系，并说明理由．
（3）AB边上是否存在点F，使得EF⊥AE？若存在，请求出BF:FA的值；若不存在，请说明理由．
如图，小华和小丽两人玩游戏，她们准备了A、B两个分别被平均分成三个、四个扇形的转盘．游戏规则：小华转动A盘、小丽转动B盘．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．两个转盘停止后指针所指区域内的数字之和小于6，小华获胜．指针所指区域内的数字之和大于6，小丽获胜． 
（1）用树状图或列表法求小华、小丽获胜的概率；
（2）这个游戏规则对双方公平吗？请判断并说明理由．
如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴于A．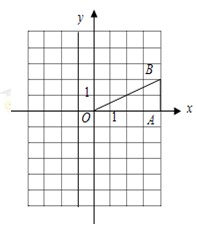
（1）画出将△OAB绕原点逆时针旋转90°后所得的△OA1B1，并写出点A1、B1的坐标；
（2）作△OAB关于原点O的中心对称图形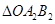
，写出对称点
、
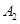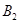的坐标．
将分别标有数学2，3，5的三张质地，大小完全一样的卡片背面朝上放在桌面上，
（1）随机抽取一张，求抽到奇数的概率；
（2）随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字，能组成哪些两位数？并求出抽取到的两位数恰好是35的概率．
确定下列抛物线的开口方向、对称轴和顶点坐标
（1）
（2）
解方程
（1）
（2）x2﹣5x﹣6="0"