某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙,地面利用原地面均不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,屋顶每平方米造价20元.
(1)仓库面积 的最大允许值是多少?
的最大允许值是多少?
(2)为使面积 达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)现给出三个条件:① ;②
;② ;③
;③ .试从中选出两个可以确定
.试从中选出两个可以确定 的条件,写出你的选项,并以此为依据求出
的条件,写出你的选项,并以此为依据求出 的面积(只需写出一个选定方案即可).
的面积(只需写出一个选定方案即可).
已知 是等差数列,其前
是等差数列,其前 项和为
项和为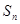 ;
; 是等比数列,且
是等比数列,且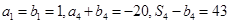 .
.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
如图,要计算东湖岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,试求两景点
,试求两景点 与
与 的距离.
的距离.
已知不等式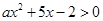 的解集是
的解集是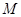 .
.
(1)若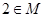 ,求
,求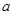 的取值范围;
的取值范围;
(2)若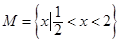 ,求不等式
,求不等式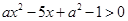 的解集.
的解集.