(本小题满分14分)设函数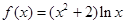 ,
,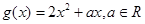
(1)证明: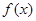 是
是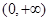 上的增函数;
上的增函数;
(2)设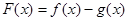 ,当
,当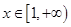 时,
时,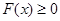 恒成立,求
恒成立,求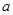 的取值范围.
的取值范围.
如图,四棱锥P-ABCD中,AD∥BC,∠ADC= ,
,
PC⊥平面ABCD,点E为AB中点。AC⊥DE,
其中AD=1,PC=2,CD= ;
;
(1)求异面直线DE与PB所成角的余弦值;
(2)求直线PC与平面PDE所成角的余弦值。
已知二项式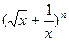 的展开式中各项系数和为64.
的展开式中各项系数和为64.
(Ⅰ)求 ; (Ⅱ)求展开式中的常数项
; (Ⅱ)求展开式中的常数项
在 中,角A,B,C所对的边分别是a,b,c,且a>b>c.设向量
中,角A,B,C所对的边分别是a,b,c,且a>b>c.设向量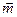 ="(cosB,sinB),"
="(cosB,sinB),"  为单位向量。
为单位向量。
(1)求角B的大小,
(2)若 ABC的面积
ABC的面积
已知函数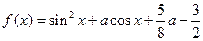 ,
, .
.
(1)当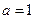 时,求函数
时,求函数 的最大值;
的最大值;
(2)如果对于区间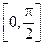 上的任意一个
上的任意一个 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
已知函数 (其中
(其中 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为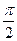 ,且图象上一个最低点为
,且图象上一个最低点为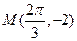 .
.
(Ⅰ)求 的解析式;(Ⅱ)当
的解析式;(Ⅱ)当 ,求
,求 的值域
的值域