已知,如图,抛物线 与
与 轴交于点C,与
轴交于点C,与 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.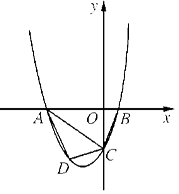
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 左侧),与 轴交于点 ,顶点为 ,对称轴与 轴交于点 .
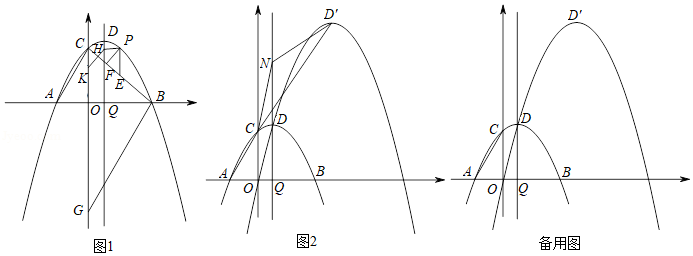
(1)如图1,连接 , .若点 为直线 上方抛物线上一动点,过点 作 轴交 于点 ,作 于点 ,过点 作 交 轴于点 .点 , 分别在对称轴和 轴上运动,连接 , .当 的周长最大时,求 的最小值及点 的坐标.
(2)如图2,将抛物线沿射线 方向平移,当抛物线经过原点 时停止平移,此时抛物线顶点记为 , 为直线 上一点,连接点 , , ,△ 能否构成等腰三角形?若能,直接写出满足条件的点 的坐标;若不能,请说明理由.
在 中, 平分 交 于点 .
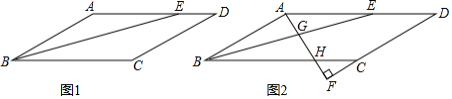
(1)如图1,若 , ,求 的面积;
(2)如图2,过点 作 ,交 的延长线于点 ,分别交 , 于点 , ,且 .求证: .
某菜市场有2.5平方米和4平方米两种摊位,2.5平方米的摊位数是4平方米摊位数的2倍.管理单位每月底按每平方米20元收取当月管理费,该菜市场全部摊位都有商户经营且各摊位均按时全额缴纳管理费.
(1)菜市场毎月可收取管理费4500元,求该菜市场共有多少个4平方米的摊位?
(2)为推进环保袋的使用,管理单位在5月份推出活动一:“使用环保袋送礼物”,2.5平方米和4平方米两种摊位的商户分别有 和 参加了此项活动.为提高大家使用环保袋的积极性,6月份准备把活动一升级为活动二:“使用环保袋抵扣管理费”,同时终止活动一.经调査与测算,参加活动一的商户会全部参加活动二,参加活动二的商户会显著增加,这样,6月份参加活动二的2.5平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加 ,毎个摊位的管理费将会减少 ;6月份参加活动二的4平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加 ,每个摊位的管理费将会减少 .这样,参加活动二的这部分商户6月份总共缴纳的管理费比他们按原方式共缴纳的管理费将减少 ,求 的值.
函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数 和 的图象如图所示.
|
|
|
|
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
|
0 |
|
|
|
|

(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点 , 的坐标和函数 的对称轴.
(2)探索思考:平移函数 的图象可以得到函数 和 的图象,分别写出平移的方向和距离.
(3)拓展应用:在所给的平面直角坐标系内画出函数 的图象.若点 , 和 , 在该函数图象上,且 ,比较 , 的大小.
在数的学习过程中,我们总会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了偶数、奇数、合数、质数等.现在我们来研究一种特殊的自然数 “纯数”.
定义:对于自然数 ,在通过列竖式进行 的运算时各位都不产生进位现象,则称这个自然数 为“纯数”.
例如:32是“纯数”,因为 在列竖式计算时各位都不产生进位现象;23不是“纯数”,因为 在列竖式计算时个位产生了进位.
(1)请直接写出1949到2019之间的“纯数”;
(2)求出不大于100的“纯数”的个数,并说明理由.