(理科)已知椭圆
 的离心率为
的离心率为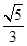 ,定点
,定点 ,椭圆短轴的端点是
,椭圆短轴的端点是 ,
, ,且
,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 且斜率不为
且斜率不为 的直线交椭圆
的直线交椭圆 于
于 ,
,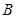 两点.试问
两点.试问 轴上是否存在定点
轴上是否存在定点 ,使
,使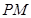 平分
平分 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分12分)甲、乙、丙三位同学彼此独立地从A、B、C、D、E五所高校中,任选2所高校参加自主招生考试(并且只能选2所高校),但同学甲特别喜欢A高校,他除选A校外,在B、C、D、E中再随机选1所;同学乙和丙对5所高校没有偏爱,都在5所高校中随机选2所即可.
(1)求甲同学未选中E高校且乙、丙都选中E高校的概率;
(2)记X为甲、乙、丙三名同学中未参加E校自主招生考试的人数,求X的分布列及数学期望.
(本小题满分12分)在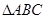 中,已知
中,已知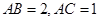 ,且cos2A+2sin
,且cos2A+2sin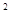
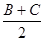 =1.
=1.
(1)求角 的大小和
的大小和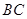 边的长;
边的长;
(2)若点 在
在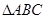 内运动(包括边界),且点
内运动(包括边界),且点 到三边的距离之和为d,设点
到三边的距离之和为d,设点 到
到 的距离分别为x,y,试用x,y表示d,并求d的取值范围.
的距离分别为x,y,试用x,y表示d,并求d的取值范围.
(本小题满分10分)选修4—5:不等式选讲
已知函数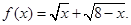
(Ⅰ)求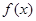 的最大值;
的最大值;
(Ⅱ)若关于x的不等式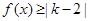 有解,求实数
有解,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
已知倾斜角为 的直线
的直线 经过点P(1,1).
经过点P(1,1).
(Ⅰ)写出直线l的参数方程;
(Ⅱ)设直线l与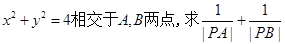 的值。
的值。
(本小题满分10分)选修4—1:几何证明选讲
如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.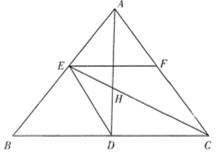
(Ⅰ)求∠B的度数;
(Ⅱ)证明:AE=4F.