(理科)已知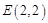 是抛物线
是抛物线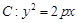 上一点,经过点
上一点,经过点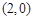 的直线
的直线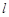 与抛物线
与抛物线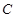 交于
交于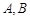 两点(不同于点
两点(不同于点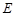 ),直线
),直线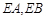 分别交直线
分别交直线 于点
于点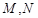 .
.
(Ⅰ)求抛物线方程及其焦点坐标;
(Ⅱ)已知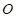 为原点,求证:
为原点,求证: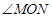 为定值.
为定值.
四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.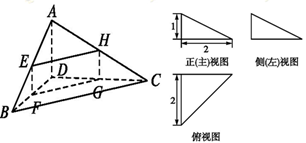
(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
已知函数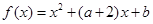 ,
,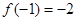 ,对于
,对于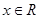 ,
,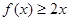 恒成立.
恒成立.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设函数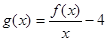 .
.
①证明:函数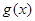 在区间在
在区间在 上是增函数;
上是增函数;
②是否存在正实数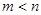 ,当
,当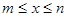 时函数
时函数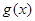 的值域为
的值域为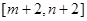 .若存在,求出
.若存在,求出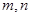 的值,若不存在,则说明理由.
的值,若不存在,则说明理由.
已知定义在区间 上的函数
上的函数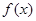 满足
满足 ,且当
,且当 时,
时,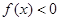 .
.
(Ⅰ)求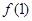 的值;
的值;
(Ⅱ)判断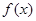 的单调性并予以证明;
的单调性并予以证明;
(Ⅲ)若 解不等式
解不等式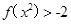 .
.
已知函数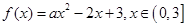 .
.
(Ⅰ)当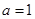 时,求函数
时,求函数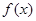 的值域;
的值域;
(Ⅱ)若集合 ,求实数
,求实数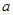 的取值范围.
的取值范围.
已知函数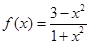 .
.
(Ⅰ)计算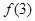 ,
,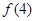 ,
,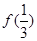 及
及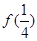 的值;
的值;
(Ⅱ)由(Ⅰ)的结果猜想一个普遍的结论,并加以证明;
(Ⅲ)求值: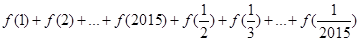 .
.