(理科)椭圆C: (a>b>0)的左、右焦点分别是F1、F2,离心率为
(a>b>0)的左、右焦点分别是F1、F2,离心率为 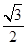 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为l.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为l.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF1、PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过点p作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明 为定值,并求出这个定值.
为定值,并求出这个定值.
在△ABC中,内角 所对的边分别是
所对的边分别是 ,且满足:
,且满足: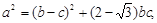 又
又 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=2,求△ABC的面积S.
已知函数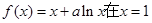 处的切线l与直线
处的切线l与直线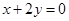 垂直,函数
垂直,函数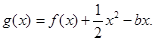
(Ⅰ)求实数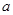 的值;
的值;
(Ⅱ)若函数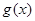 存在单调递减区间,求实数
存在单调递减区间,求实数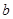 的取值范围;
的取值范围;
(Ⅲ)设 是函数
是函数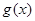 的两个极值点,若
的两个极值点,若 ,求
,求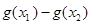 的最小值。
的最小值。
设椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆的长轴长为
的离心率互为倒数,且椭圆的长轴长为 .
.
(Ⅰ)求椭圆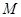 的方程;
的方程;
(Ⅱ)若直线 交椭圆
交椭圆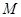 于
于 两点,
两点,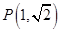 为椭圆
为椭圆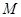 上一点,求
上一点,求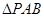 面积的最大值.
面积的最大值.
从某学校的 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 ,第二组
,第二组 ,第八组
,第八组 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人。
人。
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在 以上(含
以上(含 )的人数;
)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,事件
,事件 ,事件
,事件 ,求
,求
已知数列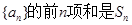 ,且
,且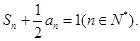
(Ⅰ)求数列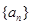 的通项公式;
的通项公式;
(Ⅱ)设 ,求适合方程
,求适合方程 的正整数
的正整数 的值。
的值。