.(本小题满分14分)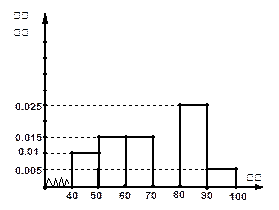
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段 ,
,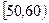 …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)用分层抽样的方法从成绩是80分以上(包括80分)的学生中抽取了6人进行试卷分析,再从这6个人中选2人作学习经验介绍发言,求选出的2人中至少有1人在 的概率.
的概率.
如果以数列 的任意连续三项作边长,都能构成一个三角形,那么称这样的数列
的任意连续三项作边长,都能构成一个三角形,那么称这样的数列 为“三角形”数列;又对于“三角形”数列
为“三角形”数列;又对于“三角形”数列 ,如果函数y=f(x)使得由
,如果函数y=f(x)使得由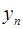 =f(
=f( )(
)(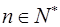 )确定的数列
)确定的数列 仍成为一个“三角形”数列,就称y="f(x)" 是数列
仍成为一个“三角形”数列,就称y="f(x)" 是数列 的“保三角形”函数。
的“保三角形”函数。
(Ⅰ)、已知数列 是首项为2012,公比为
是首项为2012,公比为 的等比数列,求证:
的等比数列,求证: 是“三角形”数列;
是“三角形”数列;
(Ⅱ)、已知数列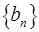 是首项为2,公差为1的等差数列,若函数f(x)=
是首项为2,公差为1的等差数列,若函数f(x)= (m>0且m≠1)是
(m>0且m≠1)是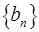 的“保三角形”函数. 求m的取值范围.
的“保三角形”函数. 求m的取值范围.
向量 =(4cos
=(4cos , sin
, sin ),
), 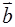 =(sin
=(sin , 4cos
, 4cos ),
), =(cos
=(cos , -4sin
, -4sin )(
)(
 且
且 、
、 均不等于
均不等于 ).
).
(Ⅰ)、求 的最大值;
的最大值;
(Ⅱ)、当 ∥
∥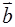 且
且  ⊥(
⊥(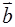 -2
-2 )时,求tan
)时,求tan + tan
+ tan 的值.
的值.
将全体正整数组成的数列1,2,3,···,n,······进行如下的分组:(1),(2,3),(4,5,6),······.即第n组含有n个正整数(n="1,2,3," ·····),记第n组各数的和为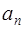 .
.
(Ⅰ)、求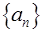 的通项
的通项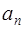 ;
;
(Ⅱ)、求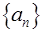 的前n项和
的前n项和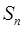 .
.
 中,过BC边的中点D作BC边的垂线
中,过BC边的中点D作BC边的垂线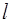 ,P是
,P是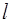 上不同于D的任一点. 记
上不同于D的任一点. 记 
 . 若
. 若 ,
,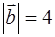 .求
.求 的值
的值
已知三个数成等差数列,其和为21,若第二个数减去1 ,第三个数加上1,则三个数成等比数列. 求原来的三个数.