(理科)已知双曲线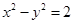 的左、右焦点分别为
的左、右焦点分别为 ,
,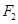 ,过点
,过点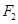 的动直线与双曲线相交于
的动直线与双曲线相交于 两点.
两点.
(Ⅰ)若动点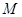 满足
满足 (其中
(其中 为坐标原点),求点
为坐标原点),求点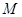 的轨迹方程;
的轨迹方程;
(Ⅱ)在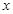 轴上是否存在定点
轴上是否存在定点 ,使
,使 ·
· 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分10分)选修4-4:坐标系于参数方程
在直角坐标系 中,以O为极点,x正半轴为极轴建立极坐标系,曲线
中,以O为极点,x正半轴为极轴建立极坐标系,曲线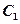 的极坐标方程为
的极坐标方程为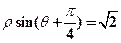 ,M,N分别为
,M,N分别为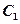 与x轴,y轴的交点。曲线
与x轴,y轴的交点。曲线 的参数方程为
的参数方程为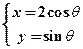 (
(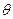 为参数)。
为参数)。
(Ⅰ)求M,N的极坐标,并写出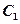 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求N点与曲线 上的动点距离的最大值。
上的动点距离的最大值。
(本小题满分10分)
选修4-1:几何证明选讲
自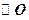 外一点p引切线与
外一点p引切线与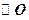 切于点A,M为PA的中点,过M引割线交
切于点A,M为PA的中点,过M引割线交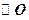 于B、C两点。
于B、C两点。
求证:
(Ⅰ) ;
;
(Ⅱ)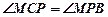 。
。
已知函数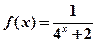
 。
。
(Ⅰ)试证函数f(x)的图象关于点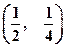 对称;
对称;
(Ⅱ)若数列 的通项公式为
的通项公式为 , 求数列
, 求数列 的前
的前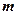 项和
项和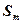 ;
;
(Ⅲ)设数列 满足:
满足: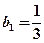 ,
, 。设
。设 。若(Ⅱ)中的
。若(Ⅱ)中的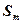 满足对任意不小于2的正整数
满足对任意不小于2的正整数 ,
, 恒成立,试求
恒成立,试求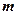 的最大值。
的最大值。
已知抛物线、椭圆和双曲线都经过点 ,它们在
,它们在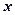 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求这三条曲线的方程;
(Ⅱ)已知动直线l过点P(3,0),交抛物线于A、B两点,是否存在垂直于X轴的直线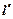 被以AP为直径的圆截得的弦长为定值?若存在,求出
被以AP为直径的圆截得的弦长为定值?若存在,求出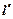 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
(本小题满分12分)假设某奶粉是经过A、B、C三道工序加工而成的,A、B、C工序的产品合格率分别为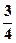 、
、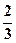 、
、 。已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场。
。已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场。
(Ⅰ)正式生产前先试生产2袋奶粉,求这2袋奶粉都为废品的概率;
(Ⅱ)设 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求 的分布列和数学期望。
的分布列和数学期望。