已知函数 .
.
(1)用“五点法”画出函数f(x)在[0, ]上的简图;
]上的简图;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,f(A)=1, ,b+c=3(b>c),求b,c的长.
,b+c=3(b>c),求b,c的长.
已知不等式 .
.
(1)当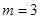 时解此不等式;
时解此不等式;
(2)若对于任意的实数 ,此不等式恒成立,求实数
,此不等式恒成立,求实数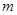 的取值范围.
的取值范围.
设函数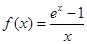 ,
,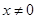 .
.
(1)判断函数 在
在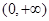 上的单调性;
上的单调性;
(2)证明:对任意正数a,存在正数x,使不等式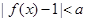 成立.
成立.
已知数列 中
中 ,函数
,函数 .
.
(1)若正项数列 满足
满足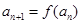 ,试求出
,试求出 ,
, ,
, ,由此归纳出通项
,由此归纳出通项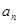 ,并加以证明;
,并加以证明;
(2)若正项数列 满足
满足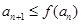 (n∈N*),数列
(n∈N*),数列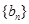 的前项和为Tn,且
的前项和为Tn,且 ,求证:
,求证: .
.
为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(Ⅰ)求该产品不能销售的概率;
(Ⅱ)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利﹣80元).已知一箱中有产品4件,记一箱产品获利X元,求X的分布列,并求出均值E(X).
已知函数 在
在 处取得极值.
处取得极值.
(1)求a、b的值;
(2)求过点 且与曲线
且与曲线 相切的切线方程.
相切的切线方程.