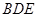如图,在四棱柱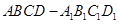 中,底面
中,底面 是等腰梯形,
是等腰梯形,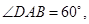
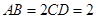 ,
,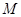 是线段
是线段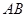 的中点.
的中点.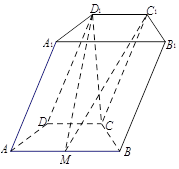
(Ⅰ)求证: ;
;
(Ⅱ)若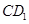 垂直于平面
垂直于平面 且
且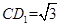 ,求平面
,求平面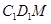 和平面
和平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
已知三棱锥P—ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB。
(1)求证明:MN⊥AB;
(2)当∠APB=90°,BC=2,AB=4时,求MN的长。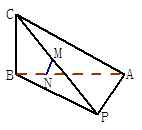
如图,在四棱锥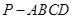 中,
中,
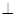 平面
平面 ,底面
,底面 是菱形,
是菱形, .
.
(1)求证: 平面
平面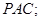
(2)若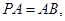 求
求 与
与 所成角的余弦值;
所成角的余弦值;
如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.
求证:(1)CD⊥PD;(2)EF⊥平面PCD.
如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.
(1)求证:BC∥l;
(2)MN与平面PAD是否平行?试证明你的结论。
如图,在正方体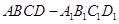 中,
中,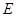 是
是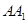 的中点,求证:
的中点,求证: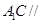 平面
平面