设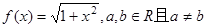 ,求证:
,求证: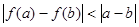
 分别是椭圆
分别是椭圆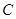 :
: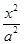 +
+ =1(
=1(
 )的左、右焦点,
)的左、右焦点, 是椭圆
是椭圆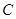 的上顶点,
的上顶点,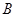 是直线
是直线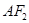 与椭圆
与椭圆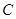 的另一个交点,
的另一个交点,

 =60°.
=60°.
(1)求椭圆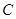 的离心率;
的离心率;
(2)已知△
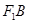 的面积为40
的面积为40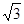 ,求a, b 的值.
,求a, b 的值.
已知椭圆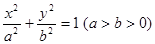 ,点
,点 在椭圆上。
在椭圆上。
(1)求椭圆的离心率;
(2)若椭圆的短半轴长为 ,直线
,直线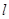 与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线
与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线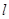 的方程。
的方程。
已知椭圆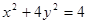 ,直线
,直线 :y=x+m
:y=x+m
(1)若 与椭圆有一个公共点,求
与椭圆有一个公共点,求 的值;
的值;
(2)若 与椭圆相交于P,Q两点,且|PQ|等于椭圆的短轴长,求m的值.
与椭圆相交于P,Q两点,且|PQ|等于椭圆的短轴长,求m的值.
设命题 ;命题
;命题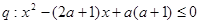 ,若
,若 是
是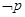 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
若椭圆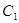 的离心率为
的离心率为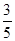 ,焦点在
,焦点在 轴上,且长轴长为10,曲线
轴上,且长轴长为10,曲线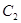 上的点与椭圆
上的点与椭圆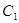 的两个焦点的距离之差的绝对值等于4.
的两个焦点的距离之差的绝对值等于4.
(1)求椭圆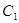 的标准方程;
的标准方程;
(2)求曲线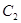 的方程。
的方程。