某车间有10名工人,其中4人仅会车工,3人仅会钳工,另外3人车、钳工都会,现需选出6人完成一件,需要车工、钳工各3人,问有多少种选派方案?
分析:如果先考虑钳工,因有6人会钳工,故有C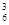 种选法,但此时不清楚选出的钳工中有几个是车钳工都会的,因此也不清楚其余的7人中有多少人会车工,因此在选车工时,就无法确定是从大局出7人中选,还是从6人、5人或4人中选。同样,如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类:
种选法,但此时不清楚选出的钳工中有几个是车钳工都会的,因此也不清楚其余的7人中有多少人会车工,因此在选车工时,就无法确定是从大局出7人中选,还是从6人、5人或4人中选。同样,如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类:
(1)选出的6人中不含全能工人;
(2)选出的6人中含有一名全能工人;
(3)选出的6人中含有2名全能工人;
(4)选出的6人中含有31名全能工人;
已知向量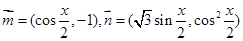 ,设函数
,设函数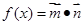 +1
+1
(1)若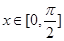 ,
, 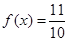 ,求
,求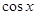 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是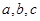 ,且满足
,且满足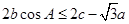 ,求
,求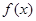 的取值范围.
的取值范围.

 已知
已知 ,
,
(1)求 解析式
解析式
(2)若函数 与
与 关于直线
关于直线 对称,若对任意实数
对称,若对任意实数
恒有 成立,求
成立,求 取值范围
取值范围
已知函数 ,
, 图象与x轴交点中,相邻两个交点之间的距离为
图象与x轴交点中,相邻两个交点之间的距离为 ,且图象最低点
,且图象最低点
(1)求 解析式
解析式
(2)将 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到 ,求
,求 的单调递减区间
的单调递减区间
函数 函数最大值为1,最小值为
函数最大值为1,最小值为 ,求
,求
某班50名学生在一次百米测试中,成绩介于13秒与18秒之间。将测试结果分成五组,按上述分组方法得到如下频率分布直方图
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数
(2) 表示该班两位同学百米测试成绩且
表示该班两位同学百米测试成绩且 ,求
,求 的概率
的概率