已知{an}是公比为q的等比数列,且a1,a3,a2成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
设

(1)若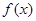 在[1,
在[1,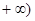 上递增,求
上递增,求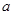 的取值范围;
的取值范围;
(2)求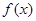 在[1,4]上的最小值
在[1,4]上的最小值
车站每天8∶00-9∶00,9∶00-10∶00都恰有一辆客车到站,8∶00-9∶00到站的客车A可能在8∶10,8∶30,8∶50到站,其概率依次为 ;9∶00-10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为
;9∶00-10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为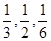 .
.
(1)旅客甲8∶00到站,设他的候车时间为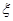 ,求
,求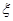 的分布列和
的分布列和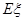 ;
;
(2)旅客乙8∶20到站,设他的候车时间为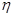 ,求
,求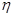 的分布列和
的分布列和 .
.
如图所示的多面体是由底面为 的长方体被截面
的长方体被截面 所截面而得到的,其中
所截面而得到的,其中 ,
, .
.
(Ⅰ)求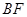 的长;
的长;
(Ⅱ)求点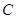 到平面
到平面 的距离.
的距离.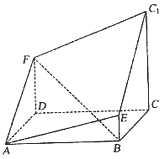
数列{ }满足
}满足
(1)若{ }是等差数列,求其通项公式;
}是等差数列,求其通项公式;
(2)若{ }满足
}满足 为{
为{ }的前
}的前 项和,求
项和,求 .
.
已知函数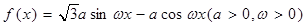 的图象上两相邻最高点的坐标分别为
的图象上两相邻最高点的坐标分别为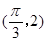 和
和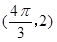
(1)求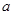 与
与 的值;
的值;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,且f (A )=2,求 的值.
的值.