(本小题满分13分)已知抛物线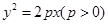 上一动点
上一动点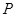 ,抛物线内一点
,抛物线内一点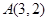 ,
,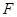 为焦点且
为焦点且 的最小值为
的最小值为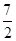 。
。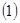 求抛物线方程以及使得|PA|+|PF|最小时的P点坐标;
求抛物线方程以及使得|PA|+|PF|最小时的P点坐标;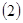 过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点? 若是,求出该定点坐标; 若不是,请说明理由。
过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点? 若是,求出该定点坐标; 若不是,请说明理由。
(本小题满分15分)如果数列 同时满足以下两个条件:(1)各项均不为0;(2)存在常数
同时满足以下两个条件:(1)各项均不为0;(2)存在常数 ,
,
对任意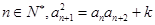 都成立,则称这样的数列
都成立,则称这样的数列 为“
为“ 类等比数列”.
类等比数列”.
(Ⅰ)若数列 满足
满足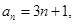 证明数列
证明数列 为“
为“ 类等比数列”,并求出相应的
类等比数列”,并求出相应的 的值;
的值;
(Ⅱ)若数列 为“
为“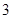 类等比数列”,且满足
类等比数列”,且满足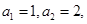 问是否存在常数
问是否存在常数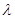 ,使得
,使得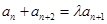 对
对
任意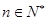 都成立?若存在,求出
都成立?若存在,求出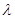 ,若不存在,请举出反例.
,若不存在,请举出反例.
(本小题满分15分) 如图,设椭圆 的左、右焦点分别为
的左、右焦点分别为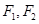 ,过
,过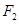
作直线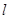 交椭圆与
交椭圆与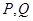 两点,若圆
两点,若圆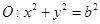 过
过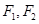 ,且
,且 的周长为
的周长为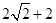 .
.
(Ⅰ)求椭圆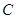 和圆
和圆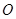 的方程;
的方程;
(Ⅱ)若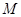 为圆
为圆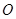 上任意一点,设直线
上任意一点,设直线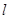 的方程为:
的方程为: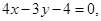 求
求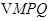 面积
面积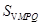 的最大值.
的最大值.
如图,已知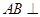 平面
平面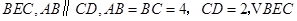 为等
为等
边三角形. 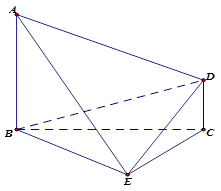
(Ⅰ)求证:平面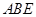 ⊥平面
⊥平面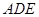 ;
;
(Ⅱ)求二面角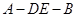 的平面角的余弦值.
的平面角的余弦值.
在△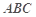 中,角
中,角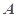 、
、 、
、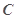 的对边分别为
的对边分别为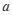 、
、 、
、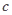 ,且满足
,且满足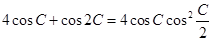 .
.
(Ⅰ)求角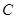 的大小;
的大小;
(Ⅱ)若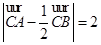 ,求
,求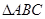 面积的最大值.
面积的最大值.
已知函数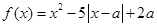 .
.
(Ⅰ)若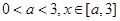 ,求
,求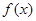 的单调区间;
的单调区间;
(Ⅱ)若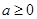 ,且存在实数
,且存在实数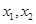 满足
满足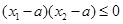 ,
,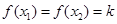 .设
.设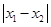 的最大值为
的最大值为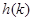 ,求
,求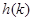 的取值范围(用
的取值范围(用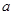 表示).
表示).