已知圆x2+y2=1和双曲线(x-1)2-y2=1,直线l与双曲线交于不同两点A、B,且线段AB的中点恰是l与圆相切的切点,求直线l的方程.
某建筑公司用8000万元购得一块空地,计划在该地块上建造一栋至少12层、每层4000平方米的楼房。经初步估计得知,如果将楼房建为x(x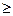 12)层,则每平方米的平均建筑费用为Q(x)=3000+50x(单位:元),为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费最小值是多少?
12)层,则每平方米的平均建筑费用为Q(x)=3000+50x(单位:元),为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费最小值是多少?
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
(1)求n的值;
(2)若高一全体学生平均每天晚自习自主支配学习时间少于45分钟,则学校需要减少作业量.根据以上抽样调查数据,学校是否需要减少作业量?
(注:统计方法中,同一组数据常用该组区间的中点值作为代表)
(3)问卷调查完成后,学校从第3组和第4组学生中利用分层抽样的方法抽取7名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取两名学生聘为学情调查联系人。求第3组中至少有1名学生被聘为学情调查联系人的概率。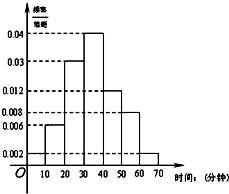
已知数列 中,
中,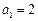 ,且
,且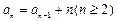 ,求这个数列的第m项
,求这个数列的第m项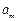 的值
的值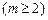 .现给出此算法流程图的一部分如图。
.现给出此算法流程图的一部分如图。
(1)请将空格部分(两个)填上适当的内容;
(2)用“For”循环语句写出对应的算法;
(3)若输出S=16,则输入的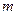 的值是多少?
的值是多少?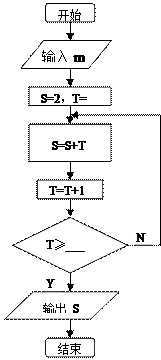
教室内有5个学生,分别佩戴1号到5号的校徽,任选3人记录他们的校徽号码。
(1)求最小号码为2的概率;(2)求三个号码中至多有一个偶数的概率
已知数列 的各项均为正数,观察程序框图,若
的各项均为正数,观察程序框图,若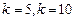 时,分别有
时,分别有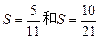 .
.
(1)试求数列 的通项;
的通项;
(2)令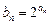 ,求
,求 的值.
的值.