某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
(1)求n的值;
(2)若高一全体学生平均每天晚自习自主支配学习时间少于45分钟,则学校需要减少作业量.根据以上抽样调查数据,学校是否需要减少作业量?
(注:统计方法中,同一组数据常用该组区间的中点值作为代表)
(3)问卷调查完成后,学校从第3组和第4组学生中利用分层抽样的方法抽取7名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取两名学生聘为学情调查联系人。求第3组中至少有1名学生被聘为学情调查联系人的概率。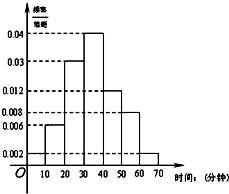
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,.求a和b至少有一人上台抽奖的概率;
已知椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左焦点为
的左焦点为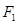 ,右焦点为
,右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 于点
于点 ,线段
,线段 垂直平分线交
垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程;
的方程;
(3)设第(2)问中的 与
与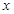 轴交于点
轴交于点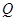 ,不同的两点
,不同的两点 在
在 上,且满足
上,且满足 ,求
,求 的取值范围.
的取值范围.
如图,已知四棱锥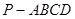 中,底面
中,底面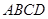 为菱形,
为菱形, 平面
平面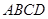 ,
, ,
,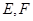 分别是
分别是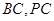 的中点.
的中点.
(1)证明: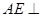 平面
平面 ;
;
(2)取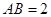 ,若
,若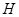 为
为 上的动点,
上的动点, 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值。
的余弦值。
已知命题 “存在
“存在 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”
表示双曲线”
(1)若“ 且
且 ”是真命题,求
”是真命题,求 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、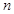 人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.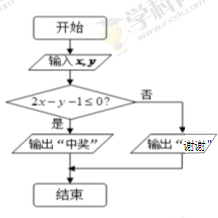
(1)求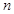 的值;
的值;
(2)把在前排就坐的高二代表队6人分别记为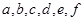 ,现随机从中抽取2人上台抽奖,
,现随机从中抽取2人上台抽奖,
求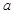 和
和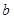 至少有一人上台抽奖的概率;
至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个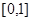 之间的均匀随机数
之间的均匀随机数 ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.