(本小题满分12分)已知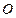 为坐标原点,向量
为坐标原点,向量
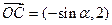 ,点
,点 满足
满足 .
.
(1)记函数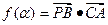 ,求函数
,求函数 的最小正周期;
的最小正周期;
(2)若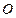 、
、 、
、 三点共线,求
三点共线,求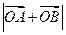 的值.
的值.
(本小题满分12分)记函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 .
.
(1)求 ;
;
(2)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分14分) 如果对于函数 的定义域内的任意
的定义域内的任意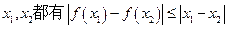 成立,那么就称函数
成立,那么就称函数 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数 ,
,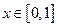 是否是 “平缓函数”?
是否是 “平缓函数”?
(2)若函数 是闭区间
是闭区间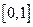 上的“平缓函数”,且
上的“平缓函数”,且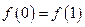 .证明:对任意的
.证明:对任意的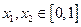 都有
都有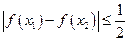 .
.
(本小题满分14分) 已知圆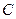 经过坐标原点, 且与直线
经过坐标原点, 且与直线 相切,切点为
相切,切点为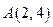 .
.
(1)求圆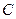 的方程;
的方程;
(2)若斜率为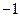 的直线
的直线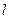 与圆
与圆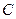 相交于不同的两点
相交于不同的两点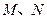 , 求
, 求 的取值范围..
的取值范围..
(本小题满分14分) 设数列 的前n项和为
的前n项和为 ,点
,点 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设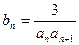 ,
, 是数列
是数列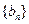 的前n项和,求使得
的前n项和,求使得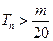 对所有
对所有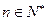 都成立的最大正整数
都成立的最大正整数 .
.