(本小题满分13分)某运动队拟在2015年3月份安排5次体能测试,规定:依次测试,只需有一次测试合格就不必参加后续的测试.已知运动员小刘5次测试每次合格的概率依次构成一个公差为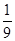 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为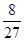 .
.
(Ⅰ)求小刘第一次参加测试就合格的概率;
(Ⅱ)在小刘参加第一、第二次测试均不合格的前提下,记小刘参加后续测试的次数为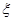 ,求随机变量
,求随机变量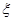 的分布列和数学期望.
的分布列和数学期望.
在△ABC中,a, b, c分别为内角A, B, C的对边,且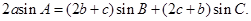
(Ⅰ)求A的大小; (Ⅱ)求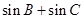 的最大值.
的最大值.
如图,已知正三棱柱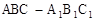 的各条棱长都为a,P为
的各条棱长都为a,P为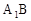 上的点。
上的点。
(1)试确定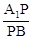 的值,使得PC⊥AB;
的值,使得PC⊥AB;
(2)若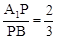 ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小;
(3)在(2)的条件下,求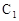 到平面PAC的距离。
到平面PAC的距离。
已知点F(0,1),直线l:y=-1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且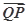 ·
·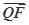 =
=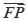 ·
·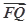 .
.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1,|DB|=l2,求 的最大值.
的最大值.
投掷一个质地均匀,每个面上标有一个数字的正方体玩具,它的六个面中,有两个面的数字是 ,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域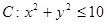 上的概率;
上的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
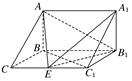
如图,在直三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,AB⊥平面BB1C1C.
(1)求直线C1B与底面ABC所成角的正切值;
(2)在棱CC1(不包括端点C、C1)上确定一点E的位置,使EA⊥EB1(要求说明理由);
(3)在(2)的条件下,若AB=,求二面角A-EB1-A1的大小.