(本小题满分15分)已知二次函数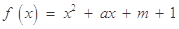 ,关于
,关于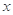 的不等式
的不等式 的解集为
的解集为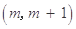 ,(
,( ),设
),设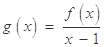 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数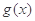 的一个极值点是
的一个极值点是 ,求
,求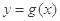 的值域;
的值域;
(Ⅲ)若函数 存在三个极值点,求
存在三个极值点,求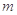 的取值范围.
的取值范围.
在数列 中,
中, ,
,
(I)求数列 的通项公式;
的通项公式;
(II)求数列 的前
的前 项和
项和
已知数列 的各项均为正数,Sn为其前n项和,对于任意
的各项均为正数,Sn为其前n项和,对于任意 ,满足关系
,满足关系 .
.
(Ⅰ)证明: 是等比数列;
是等比数列;
(Ⅱ)在正数数列 中,设
中,设 ,求数列
,求数列 中的最大项.
中的最大项.
在△ABC中,A最大,C最小,且A=2C,a+c=2b,求此三角形的三边之比.
已知方程tan2x一 tan x+1=0在x
tan x+1=0在x [0,n
[0,n )( n
)( n N*)内所有根的和记为an
N*)内所有根的和记为an
(1)写出an的表达式;(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn;
(3)设bn =(kn一5)  ,若对任何n
,若对任何n N* 都有an
N* 都有an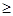 bn,求实数k的取值范围.
bn,求实数k的取值范围.
已知数列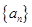 的前n项和
的前n项和 (n为正整数)。
(n为正整数)。
(Ⅰ)令 ,求证数列
,求证数列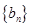 是等差数列,并求数列
是等差数列,并求数列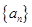 的通项公式;
的通项公式;
(Ⅱ)令 ,
,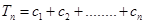 试比较
试比较 与
与 的大小,并予以证明。
的大小,并予以证明。