为了决定谁将获得仅有的一张科普报告入场劵,甲和乙设计了如下的摸球游戏:在不透明口袋中放入编号分别为1、2、3的三个红球及编号为4的一个白球,四个小球除了颜色和编号不同外,其它没有任何区别,摸球之前将袋内的小球搅匀,甲先摸两次,每次摸出一个球(第一次摸后不放回)把甲摸出的两个球放回口袋后,乙再摸,乙只摸一次且摸出一个球,如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分,如果乙摸出的球是白色,乙得1分,否则乙得0分,得分高的获得入场卷,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)请你用所学的知识说明这个游戏是否公平?
如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.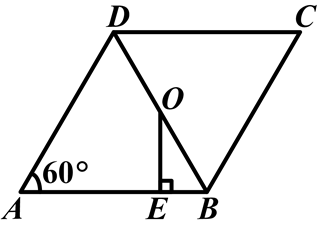
(1)求∠ABD的度数;
(2)求线段BE的长.
如图,平行四边形ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,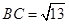 .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?
如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证: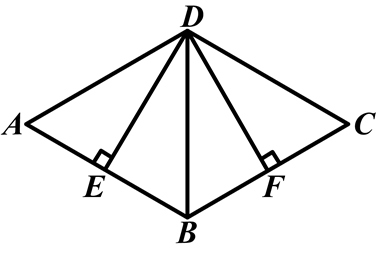
(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
如图所示,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.求证:AE=AF.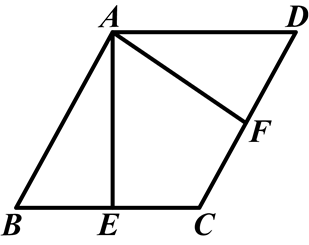
如图,四边形ABCD中,AB=CD,G,H分别是BC,AD的中点,BA,CD的延长线分别交GH的延长线于点E,F.猜想∠AEH与∠F的关系,并说明理由.