将﹣15,﹣12,﹣9,﹣6,﹣3,0,3,6,9填入下列小方格,使横,竖,斜对角的三个数字的和相等.
| |
|
|
| |
|
|
| |
|
|
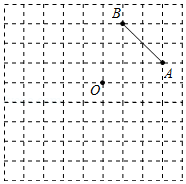
如图,在边长均为1个单位长度的小正方形组成的网格中,点 ,点 ,点 均为格点(每个小正方形的顶点叫做格点).
(1)作点 关于点 的对称点 ;
(2)连接 ,将线段 绕点 顺时针旋转 得点 对应点 ,画出旋转后的线段 ;
(3)连接 ,求出四边形 的面积.
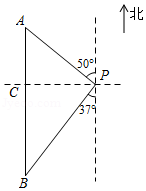
如图,热气球位于观测塔 的北偏西 方向,距离观测塔 的 处,它沿正南方向航行一段时间后,到达位于观测塔 的南偏西 方向的 处,这时, 处距离观测塔 有多远?(结果保留整数,参考数据: , , , , , .
(1)如图,已知线段 和点 ,利用直尺和圆规作 ,使点 是 的内心(不写作法,保留作图痕迹);
(2)在所画的 中,若 , , ,则 的内切圆半径是 .

如图,在平面直角坐标系中,矩形 的边 长是 的根,连接 , ,并过点 作 ,垂足为 ,动点 从 点以每秒2个单位长度的速度沿 方向匀速运动到 点为止;点 沿线段 以每秒 个单位长度的速度由点 向点 匀速运动,到点 为止,点 与点 同时出发,设运动时间为 秒 .
(1)线段 ;
(2)连接 和 ,求 的面积 与运动时间 的函数关系式;
(3)在整个运动过程中,当 是以 为腰的等腰三角形时,直接写出点 的坐标.

某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克 元,售价每千克16元;乙种蔬菜进价每千克 元,售价每千克18元.
(1)该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元,求 , 的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜 千克 为正整数),求有哪几种购买方案.
(3)在(2)的条件下,超市在获得的利润取得最大值时,决定售出的甲种蔬菜每千克捐出 元,乙种蔬菜每千克捐出 元给当地福利院,若要保证捐款后的利润率不低于 ,求 的最大值.