已知方程组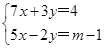
的解能使等式4x-3y=7成立．
（1）求原方程组的解；
（2）求代数式m2-2m+1的值．
如图，要用一块长4米、宽2米的长方形木板，拼接出一块长5米、宽1．5米的长方形木板，为了保证牢固，要求接缝条数尽可能地少．你能用自己学过的图形全等的有关知识设计一个拼接方案吗？
如图，延长△ABC的各边，使得BF＝AC，AE＝CD＝AB，顺次连接点D、E、F，得到△DEF为等边三角形．
（1）试说明△AEF≌△CDE；
（2）△ABC是等边三角形吗？请说明你的理由．
如图，AB∥ED，点F、C在AD上，AB＝DE，AF＝DC，试说明BC＝EF．
如图，△ABO≌△CDO，点B在CD上，AO∥CD，∠BOD＝30°，求∠A的度数．
如图（1），把大小为4×4的正方形方格图形分割成两个全等图形，请在图（2）中，沿着虚线画出四种不同的分法，把4×4的正方形方格图形分割成两个全等图形．